
【题目】如图所示,三棱锥P﹣ABC中,PA⊥平面ABC,△ABC为正三角形,PA=AB,E是PC的中点,则异面直线AE和PB所成角的余弦值为( ) 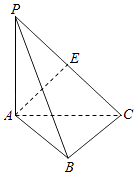
A.![]()
B.![]()
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】设f:A→B是A到B的一个映射,其中 ![]() ,f:(x,y)→(x-y,x+y),求与A中的元素(-1,2)相对应的B中的元素和与B中的元素(-1,2)相对应的A中的元素.
,f:(x,y)→(x-y,x+y),求与A中的元素(-1,2)相对应的B中的元素和与B中的元素(-1,2)相对应的A中的元素.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,平面 ![]() 平面
平面 ![]() ,四边形
,四边形 ![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.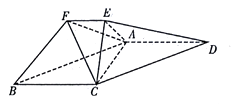
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)求 ![]() 到平面
到平面 ![]() 的距离;
的距离;
(3)求三棱锥 ![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(m2-m-1)x-5m-3,m为何值时,f(x):
(1)是幂函数;
(2)是正比例函数;
(3)是反比例函数;
(4)是二次函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知隧道的截面是半径为4.0 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m、高为3 m的货车能不能驶入这个隧道?假设货车的最大宽度为a m,那么要正常驶入该隧道,货车的限高为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
E是PC的中点.求证:

(Ⅰ)CD⊥AE;
(Ⅱ)PD⊥平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A′B′C′D′中:
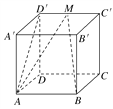
(1)求二面角D′-AB-D的大小;
(2)若M是C′D′的中点,求二面角M-AB-D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A(n)表示正整数n的个位数,an=A(n2)﹣A(n),A为数列{an}的前202项和,函数f(x)=ex﹣e+1,若函数g(x)满足f[g(x)﹣ ![]() ]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com