
 如图,在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.
如图,在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.分析 (1)证明AF⊥平面CDE.以F为原点,过F平行于DE的直线为x轴,FC,FA所在直线为y轴,z轴建立空间直角坐标系,求出相关点的坐标,求出平面ABC的一个法向量$\overrightarrow{n}$,平面CDE的一个法向量,利用向量的数量积求解平面ABC与平面CDE所成二面角的大小.
(2)设AB=x,连BF,过A作AH⊥BF,垂足为H,线段AH的长即为点A到平面BCD的距离.通过在Rt△AFB中,求解AH的表达式,推出范围即可.
解答 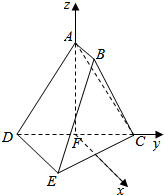 解:(1):AB⊥平面ACD,DE∥AB,可得AC=AD=CD=DE=2,F为CD的中点.DE⊥AF,AF⊥DC,
解:(1):AB⊥平面ACD,DE∥AB,可得AC=AD=CD=DE=2,F为CD的中点.DE⊥AF,AF⊥DC,
∴AF⊥平面CDE.
以F为原点,过F平行于DE的直线为x轴,FC,FA所在直线为y轴,z轴建立空间直角坐标系,如图所示,
∵AC=2,∴A(0,0,$\sqrt{3}$),设AB=x,
所以B(x,0,$\sqrt{3}$),C(0,1,0)
所以$\overrightarrow{AB}$=(x,0,0),$\overrightarrow{AC}$=(0,1,-$\sqrt{3}$),
设平面ABC的一个法向量为$\overrightarrow{n}$=(a,b,c),
则由$\overrightarrow{AB}$?$\overrightarrow{n}$=0,$\overrightarrow{AC}$?$\overrightarrow{n}$=0,得a=0,b=$\sqrt{3}$c,不妨取c=1,
则$\overrightarrow{n}$=(0,$\sqrt{3}$,1).
∵AF⊥平面CDE,∴平面CDE的一个法向量为(0,0,$\sqrt{3}$).
∴cos<$\overrightarrow{n}$,$\overrightarrow{FA}$>=$\frac{\overrightarrow{n}•\overrightarrow{FA}}{\left|\overrightarrow{n}\right|\left|\overrightarrow{FA}\right|}$=$\frac{1}{2}$,
∴<$\overrightarrow{n}$,$\overrightarrow{FA}$>=60°.
∴平面ABC与平面CDE所成的二面角的大小为60°.
(2)设AB=x,则x>0.∵AB⊥平面ACD,∴AB⊥CD.
又∵AF⊥CD,AB?平面ABF,AF?平面ABF,AB∩AF=A,
∴CD⊥平面ABF.
∵CD?平面BCD,∴平面ABF⊥平面BCD.
连BF,过A作AH⊥BF,垂足为H,则AH⊥平面BCD.
线段AH的长即为点A到平面BCD的距离.
在Rt△AFB中,AB=x,AF=$\frac{\sqrt{3}}{2}$CD=$\sqrt{3}$,
∴BF=$\sqrt{3+{x}^{2}}$,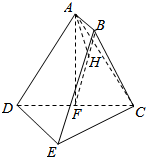
∴AH=$\frac{\sqrt{3}x}{\sqrt{3+{x}^{2}}}$=$\frac{\sqrt{3}}{\sqrt{\frac{3}{{x}^{2}}+1}}$∈(0,$\sqrt{3}$).
点评 本题考查二面角的平面角的求法,直线与平面垂直的判断,点、线、面距离的求法,可得空间想象能力以及计算能力.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
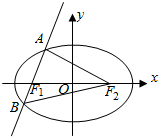 已知F1、F2为椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1(a>b>0)的左、右两个焦点,斜率不为0的直线l过左焦点F1 且交椭圆C于A(x1,y1),B(x2,y2)两点,
已知F1、F2为椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1(a>b>0)的左、右两个焦点,斜率不为0的直线l过左焦点F1 且交椭圆C于A(x1,y1),B(x2,y2)两点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
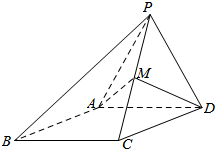 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°AB=AC=2,AA1=3.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°AB=AC=2,AA1=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
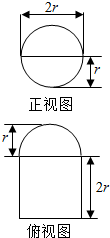 圆柱被一个平面截去一部分与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若半球的半径r=2,则该几何体的表面积为16+20π.
圆柱被一个平面截去一部分与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若半球的半径r=2,则该几何体的表面积为16+20π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 8 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com