
【题目】已知椭圆![]() 的右顶点为
的右顶点为![]() ,左焦点为
,左焦点为![]() ,离心率
,离心率![]() ,过点
,过点![]() 的直线与椭圆交于另一个点
的直线与椭圆交于另一个点![]() ,且点
,且点![]() 在
在![]() 轴上的射影恰好为点
轴上的射影恰好为点![]() ,若
,若![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,以
两点,以![]() 为直径的圆是否过定点,如过定点,求出该定点;若不过定点,请说明理由.
为直径的圆是否过定点,如过定点,求出该定点;若不过定点,请说明理由.
【答案】(1)![]() ;(2)以
;(2)以![]() 为直径的圆恒过坐标原点.
为直径的圆恒过坐标原点.
【解析】
(1)先根据离心率得![]() ,
,![]() ,再根据点B在椭圆上得B点纵坐标,最后根据三角形面积公式解得
,再根据点B在椭圆上得B点纵坐标,最后根据三角形面积公式解得![]() ,即得
,即得![]() ,(2)先考虑直线
,(2)先考虑直线![]() 的斜率不存在情况,确定定点,再利用韦达定理以及向量数量积论证圆过坐标原点.
的斜率不存在情况,确定定点,再利用韦达定理以及向量数量积论证圆过坐标原点.
(1)∵![]() ,∴
,∴![]() ,
,![]() ,
,
设![]() ,代人椭圆方程得:
,代人椭圆方程得: ![]() ,
,
∴![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)当直线![]() 的斜率不存在时,以
的斜率不存在时,以![]() 为直径的圆的圆心为
为直径的圆的圆心为![]() 或
或![]() ,半径为2,
,半径为2,
以![]() 为直径的圆的标准方程为:
为直径的圆的标准方程为: ![]() 或
或![]() ,
,
因为两圆都过坐标原点,∴以![]() 为直径的圆过坐标原点,
为直径的圆过坐标原点,
当直线![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]() ,
,![]() ,
,![]() ,
,
因为直线与圆相切,所以圆心到直线![]() 的距离,
的距离,
![]() ,
,
所以![]() ,
,
由 ,
,
化简得:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() ,
,
∴以![]() 为直径的圆过坐标原点,
为直径的圆过坐标原点,
综上,以![]() 为直径的圆恒过坐标原点.
为直径的圆恒过坐标原点.


科目:高中数学 来源: 题型:
【题目】“爱国,是人世间最深层、最持久的情感,是一个人立德之源、立功之本。”在中华民族几千年绵延发展的历史长河中,爱国主义始终是激昂的主旋律。爱国汽车公司拟对“东方红”款高端汽车发动机进行科技改造,根据市场调研与模拟,得到科技改造投入![]() (亿元)与科技改造直接收益
(亿元)与科技改造直接收益![]() (亿元)的数据统计如下:
(亿元)的数据统计如下:
| 2 | 3 | 4 | 6 | 8 | 10 | 13 | 21 | 22 | 23 | 24 | 25 |
| 13 | 22 | 31 | 42 | 50 | 56 | 58 | 68.5 | 68 | 67.5 | 66 | 66 |
当![]() 时,建立了
时,建立了![]() 与
与![]() 的两个回归模型:模型①:
的两个回归模型:模型①:![]() ;模型②:
;模型②:![]() ;当
;当![]() 时,确定
时,确定![]() 与
与![]() 满足的线性回归方程为:
满足的线性回归方程为:![]() .
.
(1)根据下列表格中的数据,比较当![]() 时模型①、②的相关指数
时模型①、②的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 182.4 | 79.2 |
(附:刻画回归效果的相关指数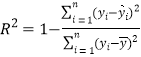 ,
,![]() .)
.)
(2)为鼓励科技创新,当科技改造的投入不少于20亿元时,国家给予公司补贴收益10亿元,以回归方程为预测依据,比较科技改造投入17亿元与20亿元时公司实际收益的大小;
(附:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式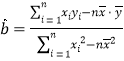
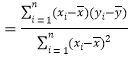 ;
;![]() )
)
(3)科技改造后,“东方红”款汽车发动机的热效![]() 大幅提高,
大幅提高,![]() 服从正态分布
服从正态分布![]() ,公司对科技改造团队的奖励方案如下:若发动机的热效率不超过
,公司对科技改造团队的奖励方案如下:若发动机的热效率不超过![]() ,不予奖励;若发动机的热效率超过
,不予奖励;若发动机的热效率超过![]() 但不超过
但不超过![]() ,每台发动机奖励2万元;若发动机的热效率超过
,每台发动机奖励2万元;若发动机的热效率超过![]() ,每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
,每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
(附:随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,
,![]() 底面
底面![]() ,
,![]() 是
是![]() 上的任意一点.
上的任意一点.
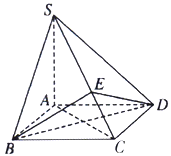
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() ,是否存在点
,是否存在点![]() 使平面
使平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ?如果存在,求出点
?如果存在,求出点![]() 的位置,如果不存在,请说明理由.
的位置,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆
轴为非负半轴为极轴建立极坐标系,两坐标系相同的长度单位.圆![]() 的方程为
的方程为![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() , 圆
, 圆![]() 在点
在点![]() 处的切线被椭圆
处的切线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() 、
、![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
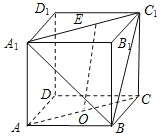
【题目】在正方体ABCD﹣A1B1C1D1中,O为线段AC的中点,点E在线段A1C1上,则直线OE与平面A1BC1所成角的正弦值的取值范围是( )
A.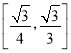 B.
B.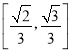 C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,近年看电子书的国人越来越多;所以近期有许多人呼呼“回归纸质书”,目前出版物阅读中纸质书占比出现上升现随机选出200人进行采访,经统计这200人中看纸质书的人数占总人数![]() .将这200人按年龄分成五组:第l组
.将这200人按年龄分成五组:第l组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,其中统计看纸质书的人得到的频率分布直方图如图所示.
,其中统计看纸质书的人得到的频率分布直方图如图所示.
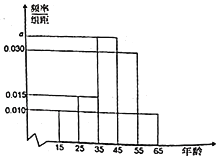
(1)求![]() 的值及看纸质书的人的平均年龄;
的值及看纸质书的人的平均年龄;
(2)按年龄划分,把年龄在![]() 的称青壮年组,年龄在
的称青壮年组,年龄在![]() 的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面
的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
看电子书 | 看纸质书 | 合计 | |
青壮年 | |||
中老年 | |||
合计 |
附:![]() (其中
(其中![]() ).
).
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com