
【题目】已知函数f(x)=|x-1|+|x+1|(x∈R).
(1)证明:函数f(x)是偶函数;
(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图象;
(3)写出函数的值域.
【答案】(1)见解析(2)见解析(3)[2,+∞).
【解析】试题分析:(1)先确定定义域关于原点对称,再根据f(-x)与f(x)相等得偶函数(2)根据绝对值定义将函数分成三段,通过描点画函数图像(3)根据函调图像可得函数最小值,无最大值,即得函数值域
试题解析:解: (1)证明:∵f(-x)=|-x-1|+|-x+1|=|-(x+1)|+|-(x-1)|=|x+1|+|x-1|=f(x),
∴函数f(x)=|x-1|+|x+1|(x∈R)为偶函数.
 (2)由x-1=0,得x=1;由x+1=0,得x=-1.
(2)由x-1=0,得x=1;由x+1=0,得x=-1.
当x<-1时,f(x)=-2x;
当-1≤x≤1时,f(x)=2;
当x>1时,f(x)=2x.
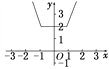
∴f(x)=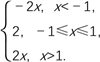 f(x)的图象如图所示.
f(x)的图象如图所示.
(3)由函数图象知,函数的值域为[2,+∞).


科目:高中数学 来源: 题型:
【题目】一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个.求:
(1)连续取两次都是红球的概率;
(2)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数![]() 的概率分布列及期望.
的概率分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2014山东.理15】已知函数![]() ,对函数
,对函数![]() ,定义
,定义![]() 关于
关于![]() 的对称函数为函数
的对称函数为函数![]() ,
,![]() 满足:对于任意
满足:对于任意![]() ,两个点
,两个点![]() 关于点
关于点![]() 对称,若
对称,若![]() 是
是![]() 关于
关于![]() 的“对称函数”,且
的“对称函数”,且![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是_________.
的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
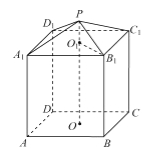
【题目】【2016高考江苏卷】现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥![]() ,下部分的形状是正四棱柱
,下部分的形状是正四棱柱![]() (如图所示),并要求正四棱柱的高
(如图所示),并要求正四棱柱的高![]() 的四倍.
的四倍.
(1)若![]() 则仓库的容积是多少?
则仓库的容积是多少?
(2)若正四棱柱的侧棱长为6m,则当![]() 为多少时,仓库的容积最大?
为多少时,仓库的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电脑公司在甲、乙两地各有一个分公司,甲分公司现有电脑6台,乙分公司现有同一型号的电脑12台.现A地某单位向该公司购买该型号的电脑10台,B地某单位向该公司购买该型号的电脑8台.已知从甲地运往A,B两地每台电脑的运费分别是40元和30元,从乙地运往A,B两地每台电脑的运费分别是80元和50元. 若总运费不超过1000元,则调运方案的种数为
A.1 B.2
C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com