【题目】某几何体的三视图如图所示，则该几何体的体积是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】根据给定的三视图可知，该几何体为如图（1）所示的几何体，是一个斜三棱柱，过点D作AC的平行线分别交
于点E,F，因为
平面
，截取
后，补到几何体左侧，使得
与
重合，构造一个以
为底面，以
为高的直三棱柱，如图（2）所示，所以
.
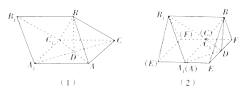
点睛: 思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：①首先看俯视图，根据俯视图画出几何体地面的直观图；②观察正视图和侧视图找到几何体前、后、左、右的高度；③画出整体，然后再根据三视图进行调整.
科目：高中数学 来源： 题型：
【题目】已知椭圆
过点
，且离心率为
.过抛物线
上一点
作
的切线
交椭圆
于
，
两点.
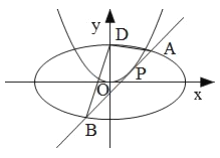
（Ⅰ）求椭圆的方程；
（Ⅱ）是否存在直线，使得
，若存在，求出的方程；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
三个班共有学生100人，为调查他们的体育锻炼情况，通过分层抽样获取了部分学生一周的锻炼时间，数据如下表（单位：小时）.
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
（Ⅰ）试估计
班学生人数；
（Ⅱ）从
班和
班抽出来的学生中各选一名，记班选出的学生为甲，班选出的学生为乙，若学生锻炼相互独立，求甲的锻炼时间大于乙的锻炼时间的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设数集
由实数构成，且满足：若
（
且
），则
.
（1）若
，试证明中还有另外两个元素；
（2）集合是否为双元素集合，并说明理由；
（3）若中元素个数不超过8个，所有元素的和为
，且中有一个元素的平方等于所有元素的积，求集合.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(2017·北京高考)由四棱柱ABCDA1B1C1D1截去三棱锥C1B1CD1后得到的几何体如图所示．四边形ABCD为正方形，O为AC与BD的交点，E为AD的中点，A1E⊥平面ABCD.
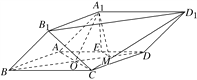
(1)证明：A1O∥平面B1CD1；
(2)设M是OD的中点，证明：平面A1EM⊥平面B1CD1.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知一元二次函数f（x）=ax2+bx+c（a＞0，c＞0）的图象与x轴有两个不同的公共点，其中一个公共点的坐标为（c，0），且当0＜x＜c时，恒有f（x）＞0．
（1）当a=1，
时，求出不等式f（x）＜0的解；
（2）求出不等式f（x）＜0的解（用a，c表示）；
（3）若以二次函数的图象与坐标轴的三个交点为顶点的三角形的面积为8，求a的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某学校准备修建一个面积为2400平方米的矩形活动场地（图中ABCD）的围栏，按照修建要求，中间用围墙EF隔开，使得ABEF为矩形，EFCD为正方形，设
米，已知围墙（包括EF）的修建费用均为每米500元，设围墙（包括EF）的修建总费用为y元．
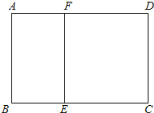
（1）求出y关于x的函数解析式及x的取值范围；
（2）当x为何值时，围墙（包括EF）的修建总费用y最小？并求出y的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
