
分析 (1)依题意知x1+x2=-m,x1x2=t,利用${T_n}=\sum_{r=0}^n{x_1^{n-r}x_2^r}$(n∈N*),易知T1=x1+x2=-m,T2=x12+x1x2+x22=(x1+x2)2-x1x2=m2-t;
(2)由Tk=$\sum_{r=0}^{k}$${{x}_{1}}^{k-r}$${{x}_{2}}^{r}$,可得T5=x1T4+x25=-mT4-tT3;
(3)利用数学归纳法证明即可.
解答 解:(1)∵x1、x2是函数f(x)=x2+mx+t的两个零点,
∴x1+x2=-m,x1x2=t,
∵${T_n}=\sum_{r=0}^n{x_1^{n-r}x_2^r}$,
∴T1=x1+x2=-m,
T2=x12+x1x2+x22=(x1+x2)2-x1x2=m2-t;
(2)证明:T5=x1$\sum_{r=0}^{4}$${{x}_{1}}^{4-r}$${{x}_{2}}^{r}$+${{x}_{2}}^{5}$=x1T4+${{x}_{2}}^{5}$,
∴T5=x1T4+${{x}_{2}}^{5}$,
x2T4=x1x2T3+${{x}_{2}}^{5}$,
故T5=x1T4+(x2T4-x1x2T3)=-mT4-tT3;
(3)证明:①当n=1,2时,由(1)知,Tk是整数,结论成立;
②假设当n=k-1,n=k(k≥2)时,结论成立,即Tk-1,Tk都是整数,
∵Tk=$\sum_{r=0}^{k}$${{x}_{1}}^{k-r}$${{x}_{2}}^{r}$,Tk+1=$\sum_{r=0}^{k+1}$${{x}_{1}}^{k+1-r}$${{x}_{2}}^{r}$,
∴同理可得,Tk+1=-mTk-tTk-1,
∵Tk-1,Tk都是整数,且m、t∈Z,
∴Tk+1也是整数;
综上所述,对任意的n∈N*,Tn∈Z.
点评 本题考查综合法证明不等式,突出考查数学归纳法的应用,考查抽象思维、逻辑思维的综合应用,考查推理证明的能力,属于难题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:选择题
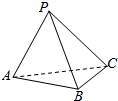
| A. | AP⊥PB,AP⊥PC | B. | AP⊥PB,BC⊥PB | ||
| C. | 平面BPC⊥平面APC,BC⊥PC | D. | AP⊥平面PBC |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com