
分析 (Ⅰ)当m=-1,化简不等式,通过x的范围,取得绝对值符号,求解不等式f(x)≤3;
(Ⅱ)利用绝对值的几何意义求解函数的最值即可.
解答 (本小题满分10分)
解:(Ⅰ)当m=-1时,不等式f(x)≤3,可化为|x-1|+|2x+1|≤3.
当$x≤-\frac{1}{2}$时,-x+1-2x-1≤3,∴x≥-1,∴$-1≤x≤-\frac{1}{2}$; (1分)
当$-\frac{1}{2}<x<1$时,-x+1+2x+1≤3,∴x≤1,∴$-\frac{1}{2}<x<1$; (2分)
当x≥1时,x-1+2x+1≤3,∴x≤1,∴x=1; (3分)
综上所得,-1≤x≤1.(4分)
(Ⅱ)$f(x)=|{x+m}|+|{2x+1}|=|{x+m}|+|{x+\frac{1}{2}}|+|{x+\frac{1}{2}}|$(5分)
$≥|{({x+m})-({x+\frac{1}{2}})}|+|{x+\frac{1}{2}}|$(6分)
=$|{m-\frac{1}{2}}|+|{x+\frac{1}{2}}|$,当且仅当$({x+m})({x+\frac{1}{2}})≤0$时等号成立.(7分)
又因为$|{m-\frac{1}{2}}|+|{x+\frac{1}{2}}|≥|{m-\frac{1}{2}}|$,当且仅当$x=-\frac{1}{2}$时,等号成立.(8分)
所以,当$x=-\frac{1}{2}$时,f(x)取得最小值$|{m-\frac{1}{2}}|$.(10分)
点评 本题考查绝对值不等式的解法,绝对值的几何意义,考查函数的最值的求法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
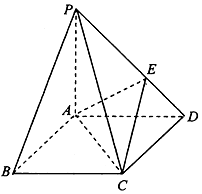 如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=$\sqrt{2}$,点E在PD上,且$\frac{PE}{ED}$=2.
如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=$\sqrt{2}$,点E在PD上,且$\frac{PE}{ED}$=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | F一定是奇数,G可能是奇数 | B. | F可能是偶数,G一定是偶数 | ||
| C. | F一定是奇数,G一定是偶数 | D. | F可能是偶数,G可能是奇数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{1+\sqrt{3}}$ | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{{2+\sqrt{3}}}{2}$ | D. | ±$\frac{{1+\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com