
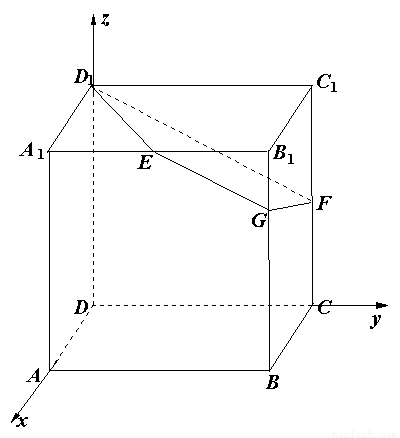
如图,已知正方体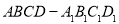 的棱长为2,E、F分别是
的棱长为2,E、F分别是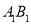 、
、 的中点,过
的中点,过 、E、F作平面
、E、F作平面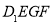 交
交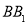 于G.
于G.
(l)求证:EG∥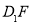 ;
;
(2)求二面角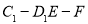 的余弦值;
的余弦值;
(3)求正方体被平面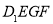 所截得的几何体
所截得的几何体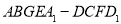 的体积.
的体积.
(1)详见试题解析(2) 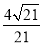 (3)
(3) 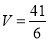
【解析】
试题分析:(1)两平行平面都与第三个平面相交,则交线平行;
(2)以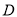 为原点分别以
为原点分别以 为
为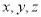 轴,建立空间直角坐标系,平面
轴,建立空间直角坐标系,平面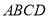 的法向量为
的法向量为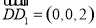 ,求出平面
,求出平面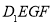 的法向量
的法向量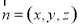
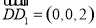 ,利用空间向量的夹角公式求二面角的余弦值.
,利用空间向量的夹角公式求二面角的余弦值.
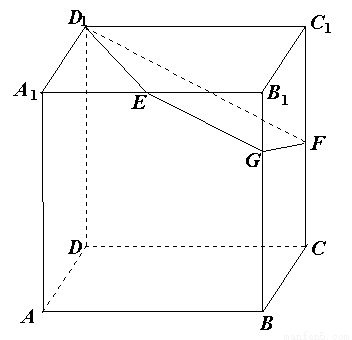
(3)所求几何体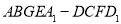 是由正方体
是由正方体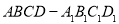 截去一个三棱台
截去一个三棱台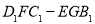 而得到, 所以,
而得到, 所以,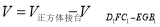 .
.
(1)证明:在正方体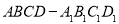 中,因为平面
中,因为平面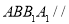 平面
平面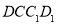 ,
,
平面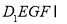 平面
平面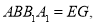 平面
平面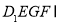 平面
平面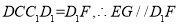
(2)【解析】
如图,以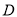 为原点分别以
为原点分别以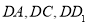 为
为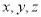 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则有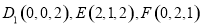
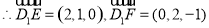
设平面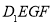 的法向量为
的法向量为 则由
则由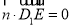 和
和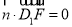 得
得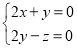
取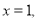 得
得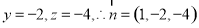
又平面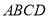 的法向量为
的法向量为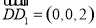
故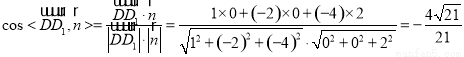
所以截面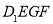 与底面
与底面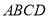 所成二面角的余弦值为
所成二面角的余弦值为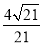
(3)【解析】
设所截几何体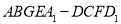 的体积为
的体积为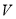
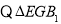 与
与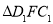 相似,
相似,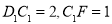
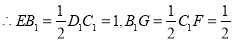

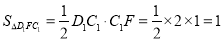
故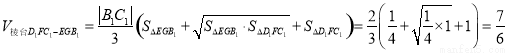
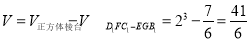
考点:1、平面与平面平行的性质;2、空间直角坐标系;3、向量夹角公式;4、组合体的体积.


科目:高中数学 来源:2013-2014学年天津市红桥区高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
设r>0,那么直线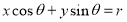 (
(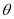 是常数)与圆
是常数)与圆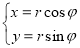 (
(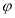 是参数)的位置关系是
是参数)的位置关系是
A.相交 B.相切 C.相离 D.视r的大小而定
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河北区高三总复习质量检测(一)文科数学试卷(解析版) 题型:选择题
已知变量x,y满足约束条件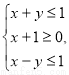 ,则目标函数z=2x +y的最大值是( ).
,则目标函数z=2x +y的最大值是( ).
(A)-4 (B)0 (C)2 (D)4
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模试卷理科数学试卷(解析版) 题型:填空题
曲线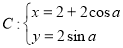 (a为参数),若以点O(0,0)为极点,x轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是____________.
(a为参数),若以点O(0,0)为极点,x轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是____________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模试卷理科数学试卷(解析版) 题型:选择题
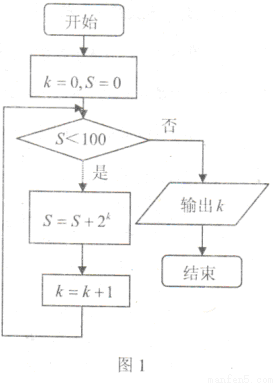
阅读图1的程序框图,该程序运行衍输出的k的值为( )
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模试卷文科数学试卷(解析版) 题型:选择题
没函数 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使 对一切实数x均成 立,则称
对一切实数x均成 立,则称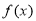 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:①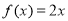 :②
:②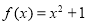 :③
:③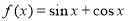 ;④
;④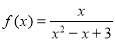 ⑤
⑤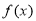 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且
对一切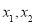 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )
A.1个 B.2个 C..3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模文科数学试卷(解析版) 题型:选择题
已知棱长为l的正方体 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 ,设面
,设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )

A. 面ABCD
面ABCD
B. AC
AC
C.面MEF与面MPQ不垂直
D.当x变化时, 不是定直线
不是定直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com