
分析 利用正切函数的周期性求得M,再利用正弦函数的定义域和值域,求得f(x)=Msin(2x-$\frac{π}{6}$)在区间[0,$\frac{π}{2}$]上的值域.
解答 解:函数g(x)=tan($\frac{π}{3}$x-$\frac{π}{6}$)的最小正周期为M=$\frac{π}{\frac{π}{3}}$=3,
当x∈[0,$\frac{π}{2}$],2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],sin(2x-$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],∴Msin(2x-$\frac{π}{6}$)=3sin(2x-$\frac{π}{6}$)∈[-$\frac{3}{2}$,3],
∴f(x)=Msin(2x-$\frac{π}{6}$)在区间[0,$\frac{π}{2}$]上的值域为[-$\frac{3}{2}$,3],
故答案为:[-$\frac{3}{2}$,3].
点评 本题主要考查正切函数的周期性,正弦函数的定义域和值域,属于基础题.


科目:高中数学 来源: 题型:解答题
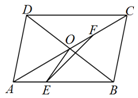 已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.
已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\overrightarrow i+2\overrightarrow j$ | B. | $-2\overrightarrow i+3\overrightarrow j$ | C. | $-3\overrightarrow i+2\overrightarrow j$ | D. | $2\overrightarrow i-3\overrightarrow j$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com