
【题目】二次函数![]() 在区间
在区间![]() 上有最大值4,最小值0.
上有最大值4,最小值0.
(1)求函数![]() 的解析式;
的解析式;
(2)设![]() ,若
,若![]() 在
在![]() 时恒成立,求
时恒成立,求![]() 的范围.
的范围.
【答案】(1)g(x)=x2﹣2x+1;(2)[33,+∞)
【解析】
(1)根据二次函数的性质讨论对称轴,即可求解最值,可得解析式.
(2)求解f(x)的解析式,f(x)﹣kx≤0在x∈[![]() ,8],分离参数即可求解.
,8],分离参数即可求解.
(1)g(x)=mx2﹣2mx+n+1(m>0)
其对称轴x=1,x∈[0,3]上,
∴当x=1时,f(x)取得最小值为﹣m+n+1=0,…①.
当x=3时,f(x)取得最大值为3m+n+1=4,…②.
由①②解得:m=1,n=0
故得函数g(x)的解析式为:g(x)=x2﹣2x+1
(2)由f(x)![]()
当x∈[![]() ,8]时,f(x)﹣kx≤0恒成立,
,8]时,f(x)﹣kx≤0恒成立,
即x2﹣4x+1﹣kx2≤0恒成立,
∴x2﹣4x+1≤kx2
∴![]() k.
k.
设![]() ,则t∈[
,则t∈[![]() ,8]
,8]
可得:1﹣4t+t2=(t﹣2)2﹣3≤k.
当t=8时,(1﹣4t+t2)max=33
故得k的取值范围是[33,+∞)


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).
(1)当![]() 时,作出
时,作出![]() 的图象,并写出它的单调递增区间;
的图象,并写出它的单调递增区间;
(2)设![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A′B′C′,∠BAC=90°,AB=AC=λAA′,点M,N分别为A′B和B′C′的中点.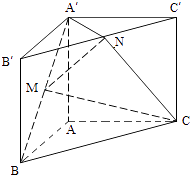
(1)证明:MN∥平面A′ACC′;
(2)若二面角A′﹣MN﹣C为直二面角,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题![]() “
“![]() ,
,![]() ”,则
”,则![]() 是真命题
是真命题
B. “![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
C. 命题“![]() ,
,![]() ”的否定是:“
”的否定是:“![]() ,
,![]() ”
”
D. “![]() ”是“
”是“![]() 在
在![]() 上为增函数”的充要条件
上为增函数”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(1)(坐标系与参数方程选做题)曲线C的直角坐标方程为x2+y2﹣2x=0,以原点为极点,x轴的正半轴为极轴建立积坐标系,则曲线C的极坐标方程为 .
(2)(不等式选做题)在实数范围内,不等式|2x﹣1|+|2x+1|≤6的解集为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.
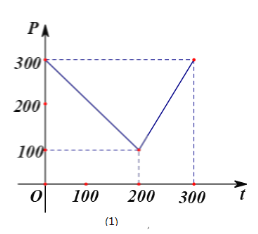
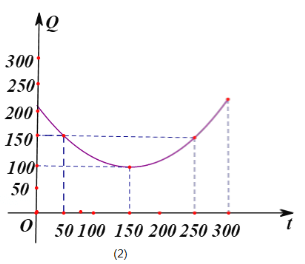
(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中,P为图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
(1)若φ= ![]() ,点P的坐标为(0,
,点P的坐标为(0, ![]() ),则ω=;
),则ω=;
(2)若在曲线段 ![]() 与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 .
与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 . 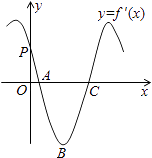
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com