
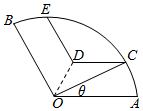
 如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.
如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.分析 (1)根据三角形的角和边的关系,利用正弦定理,求得用θ表示OD和CD的长度,利用CD的取值范围,即可求得θ的取值范围;
(2)首先将道路长度L(θ)表达成θ的函数关系式,再利用导数方法研究函数的最大值,从而可以求得θ=$\frac{π}{6}$时,观光道路最长..
解答 解:(1)AC=EB,CD∥AO.DE∥OB,
∴∠AOD=$\frac{π}{3}$,
于是在△OCD中,OC=1,∠AOB=$\frac{2π}{3}$,∠AOC=θ.∠COD=$\frac{π}{3}$-θ,
由正弦定理可知:$\frac{OD}{sin∠OCD}$=$\frac{CD}{sin∠COD}$=$\frac{OC}{sin∠CDO}$=2R,
$\frac{OD}{sinθ}$=$\frac{CD}{sin(\frac{π}{3}-θ)}$=$\frac{OC}{sin\frac{2π}{3}}$=$\frac{2\sqrt{3}}{3}$,
∴OD=$\frac{2\sqrt{3}}{3}$sinθ,CD=$\frac{2\sqrt{3}}{3}$sin($\frac{π}{3}$-θ),
∵OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$],即$\frac{\sqrt{3}}{3}$≤$\frac{2\sqrt{3}}{3}$sinθ≤$\frac{\sqrt{6}}{3}$,
∴$\frac{1}{2}$≤sinθ≤$\frac{\sqrt{2}}{2}$,
∵0<θ≤$\frac{π}{3}$,
∴$\frac{π}{6}≤θ≤\frac{π}{4}$,
故CD=$\frac{2\sqrt{3}}{3}$sin($\frac{π}{3}$-θ),($\frac{π}{6}≤θ≤\frac{π}{4}$),
(2)由(1)可知,观赏道理长L=2($\widehat{AC}$+CD)=2θ+$\frac{4\sqrt{3}}{3}$sin($\frac{π}{3}$-θ),($\frac{π}{6}≤θ≤\frac{π}{4}$),
∴L=2θ+2cosθ-$\frac{2\sqrt{3}}{3}$sinθ,
L′=2-2sinθ-$\frac{2\sqrt{3}}{3}$cosθ,
=2-$\frac{4\sqrt{3}}{3}$cos(θ-$\frac{π}{3}$),
L′=0,得cos(θ-$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$,$\frac{π}{6}≤θ≤\frac{π}{4}$,θ=$\frac{π}{6}$,
∵当$\frac{π}{6}≤θ≤\frac{π}{4}$时,$-\frac{π}{6}$<θ-$\frac{π}{3}$≤-$\frac{π}{12}$,
L′=2-$\frac{4\sqrt{3}}{3}$cos(θ-$\frac{π}{3}$)<0,
∴当θ=$\frac{π}{6}$时,L取得最大值,即观赏道路最长.
点评 本题考查解决了正弦定理,以及同角三角函数间的基本关系在实际生活中的应用,考查函数模型的构建,考查利用导数确定函数的最值,属于中档题.


科目:高中数学 来源: 题型:选择题
| x | -8 | -4 | 3 | 5 |
| y | 19 | 7 | -3 | -9 |
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知某空间几何体的三视图如图所示,若三个正方形的边长均为2,则该几何体的表面积为( )
已知某空间几何体的三视图如图所示,若三个正方形的边长均为2,则该几何体的表面积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 8$\sqrt{3}$ | D. | 12+4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com