
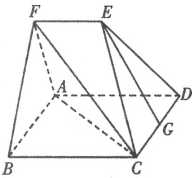
【题目】如图所示的多面体![]() 中,四边形
中,四边形![]() 为菱形,且
为菱形,且![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连结BD,交AC于M,连结FM,MG,证明![]() 即可解决问题。
即可解决问题。
(2)建立空间直角坐标系,求得平面![]() 的一个法向量
的一个法向量![]() 及
及![]() ,利用空间向量夹角公式即可求得直线EC与平面ACF所成角的正弦值,问题得解
,利用空间向量夹角公式即可求得直线EC与平面ACF所成角的正弦值,问题得解
证明:(1)连结BD,交AC于M,连结FM,MG,
因为BC=AD=2EF,EF∥BC,BC∥AD,所以![]() ,
,
在△ACD中,M,G分别为AC,CD的中点,所以![]() ,
,
所以![]() ,所以四边形EFMG是平行四边形,
,所以四边形EFMG是平行四边形,
所以EG∥FM,
又因为FM![]() 平面ACF,EC
平面ACF,EC![]() 平面ACF,所以EG∥平面ACF.
平面ACF,所以EG∥平面ACF.
(2)取AB的中点O,连结FO,OC,
因为AF=BF=BC,∠ABC=60°,四边形ABCD为菱形,所以FO⊥AB,OC⊥AB,
因为平面ABF⊥平面ABCD,所以FO⊥平面ABCD,
故以O为原点,![]() ,
,![]() ,
,![]() 分别为x轴,y轴,z轴正方向建立空间直角坐标系,设AF=BF=BC=2EF=2.
分别为x轴,y轴,z轴正方向建立空间直角坐标系,设AF=BF=BC=2EF=2.
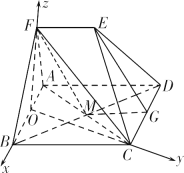
则A(-1,0,0),C(0,![]() ,0),F(0,0,
,0),F(0,0,![]() ),E(
),E(![]() ,
,![]() ,
,![]() ),
),![]() =(1,
=(1,![]() ,0),
,0),
![]() ,
,![]() ,
,
设![]() =
=![]() 是平面ACF的一个法向量,
是平面ACF的一个法向量,
则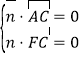 ,
,![]() ,
,
令y=z=1,则![]() ,故
,故![]() =(
=(![]() ,1,1),
,1,1),
设直线EC与平面ACF所成角为![]() ,
,
则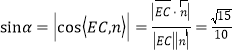 ,
,
所以直线EC与平面ACF所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】过点![]() 的椭圆
的椭圆![]() 的离心率为
的离心率为![]() ,椭圆与
,椭圆与![]() 轴交于两点
轴交于两点![]() 、
、![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求该椭圆的标准方程;
(2)当点![]() 异于点
异于点![]() 时,求证:
时,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
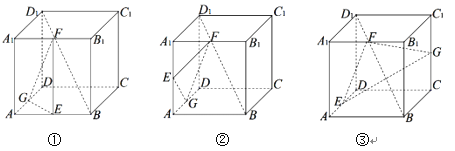
【题目】如图,在下列三个正方体![]() 中,
中,![]() 均为所在棱的中点,过
均为所在棱的中点,过![]() 作正方体的截面.在各正方体中,直线
作正方体的截面.在各正方体中,直线![]() 与平面
与平面![]() 的位置关系描述正确的是
的位置关系描述正确的是
A. ![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②③
的有且只有②③
B. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有①
的有且只有①
C. .![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②
的有且只有②
D. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有③
的有且只有③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax-2|,不等式f(x)≤4的解集为{x|-2≤x≤6}.
(1)求实数a的值;
(2)设g(x)=f(x)+f(x+3),若存在x∈R,使g(x)-tx≤2成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,PA=PD,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F.

(1)求证:EF∥平面PAB;
(2)若PB与平面ABCD所成角的正弦值为![]() ,求二面角P-AE-B的余弦值.
,求二面角P-AE-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.乘坐高铁可以网络购票,为了研究网络购票人群的年龄分布情况,在5月31日重庆到成都高铁9600名网络购票的乘客中随机抽取了120人进行了统计并记录,按年龄段将数据分成6组:![]() ,得到如图所示的直方图:
,得到如图所示的直方图:
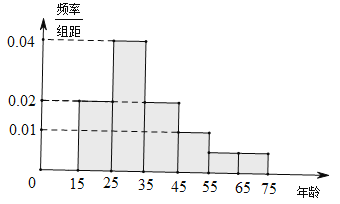
(1)若从总体的9600名网络购票乘客中随机抽取一人,估计其年龄大于35岁的概率;
(2)试估计总体中年龄在区间![]() 内的人数;
内的人数;
(3)试通过直方图,估计5月31日当天网络购票的9600名乘客年龄的中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com