
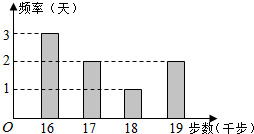
 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:| 健步走步数(前步) | 16 | 17 | 18 | 19 |
| 消耗能量(卡路里) | 400 | 440 | 480 | 520 |
分析 (I)由已知条件利用平均数公式能求出小王这8天每天“健步走”步数的平均数.
(II)设小王这2天通过“健步走”消耗的能量和不小于1000卡路里为事件A.“健步走”17千步的天数为2天,记为a1,a2,“健步走”18千步的天数为1天,记为b1,“健步走”19千步的天数为2天,记为c1,c2.利用列举法能求出小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率.
解答 解:(I) 小王这8天 每天“健步走”步数的平均数为$\frac{16×3+17×2+18×1+19×2}{8}=17.25$(千步).…(6分)
(II)设小王这2天通过“健步走”消耗的能量和不小于1000卡路里为事件A.
“健步走”17千步的天数为2天,记为a1,a2,“健步走”18千步的天数为1天,记为b1,“健步走”19千步的天数为2天,记为c1,c2.
5天中任选2天包含基本事件有:a1a2,a1b1,a1c1,a1c2,a2b1,a2c1,a2c2,b1c1,b1c2,c1c2,共10个.
事件A包含基本事件有:b1c1,b1c2,c1c2共3个.
所以$P(A)=\frac{3}{10}$.…(13分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | {-1,2} | B. | {-1} | C. | {2} | D. | $\left\{{\frac{2}{3}}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -7 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com