
【题目】若二次函数y=f(x)的图象经过原点,且1≤f(﹣1)≤2,3≤f(1)≤4,求f(﹣2)的范围.
【答案】解:因为y=f(x)的图象经过原点,所以可设y=f(x)=ax2+bx.于是 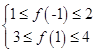 ∴
∴ ![]() (I)
(I)
解法一(利用基本不等式的性质)
不等式组(Ⅰ)变形得 ![]()
∴6≤4a﹣2b≤10,∴6≤f(﹣2)≤10,
所以f(﹣2)的取值范围是[6,10].
解法二(数形结合)
建立直角坐标系aob,作出不等式组(Ⅰ)所表示的区域,如图中的阴影部分.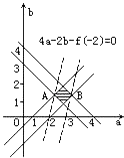
因为f(﹣2)=4a﹣2b,
所以4a﹣2b﹣f(﹣2)=0表示斜率为2的直线系.
如图,当直线4a﹣2b﹣f(﹣2)=0过点A(2,1),B(3,1)时,
分别取得f(﹣2)的最小值6,最大值10.
即f(﹣2)的取值范围是:6≤f(﹣2)≤10.
解法三(利用方程的思想)
∵ 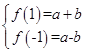 ,∴
,∴ 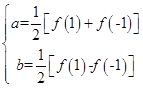
又f(﹣2)=4a﹣2b=3f(﹣1)+f(1),而
1≤f(﹣1)≤2,3≤f(1)≤4,①
所以3≤3f(﹣1)≤6.②
①+②得4≤3f(﹣1)+f(1)≤10,即6≤f(﹣2)≤10.
【解析】法一,先根据要求设出二次函数,可以利用基本不等式性质变形找出f(2)解决;法二,用数形结合思想,利用线性规划的方法求解;法三,利用方程思想反解a、b,利用f(﹣1)、f(1)来表示f(2)进而求解.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinA,cosA),
=(sinA,cosA), ![]() =(cosB,sinB),
=(cosB,sinB), ![]() =sin2C且A、B、C分别为△ABC的三边a,b,c所对的角.
=sin2C且A、B、C分别为△ABC的三边a,b,c所对的角.
(1)求角C的大小;
(2)若sinA,sinC,sinB成等比数列,且 ![]() =18,求c的值..
=18,求c的值..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD及其三视图如下图所示,E是侧棱PC上的动点.
(Ⅰ)求四棱锥P﹣ABCD的体积;
(Ⅱ)不论点E在何位置,是否都有BD⊥AE?试证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D﹣AE﹣B的大小.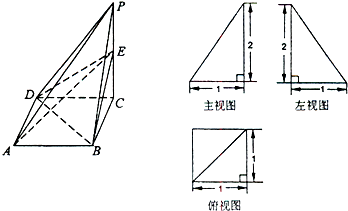
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某早餐店每天制作甲、乙两种口味的糕点共n(nN*)份,每份糕点的成本1元,售价2元,如果当天卖不完,剩下的糕点作废品处理.该早餐店发现这两种糕点每天都有剩余,为此整理了过往100天这两种糕点的日销量(单位:份),得到如下的统计数据:
甲口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 20 | 40 | 20 | 20 |
乙口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 40 | 30 | 20 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种糕点的日销量相互独立.
(1)记该店这两种糕点每日的总销量为X份,求X的分布列
(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数
①若产生浪费的概率不超过0.6,求n的最大值;
②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线![]() :
: ![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(Ⅱ)设![]() 是坐标原点,直线
是坐标原点,直线![]() 平行于
平行于![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com