
【题目】在如图所示的不规则几何体中,已知四边形![]() 是正方形,四边形
是正方形,四边形![]() 是平行四边形,平面
是平行四边形,平面![]() 平面
平面![]() ,
,![]() .
.

(1)证明:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
【答案】(1)证明见解析;(2)3
【解析】
(1)由面面垂直的性质定理得到线面垂直,再由线面垂直得到线线垂直;
(2)先建立适当的空间直角坐标系,再利用空间向量法求所求的线面角的正弦值,也可以用传统法,先找到所求角的余角,再求线面角的正切值.
(1)证明:![]() 四边形
四边形![]() 是正方形,
是正方形,![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() .
.
![]()
![]() ,
,![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() .
.
(2)解法一:建立如图所示的空间直角坐标系![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
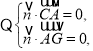

![]() ,
,
不妨令![]() ,则
,则![]() ,
,![]() 平面
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则![]() ,因为
,因为![]() ,
,![]() ,
,
故直线![]() 与平面
与平面![]() 所成角的正切值为3.
所成角的正切值为3.

解法二:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,平面
,平面![]() 平面
平面![]() ,
,
由(1)知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
![]() 平面
平面![]() ,
,![]() 即所求角的余角,令
即所求角的余角,令![]() ,
,
在![]() 中,易知
中,易知![]() ,
,
![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() ,
,
![]() ,
,
故直线![]() 与平面
与平面![]() 所成角的正切值为3.
所成角的正切值为3.



科目:高中数学 来源: 题型:
【题目】2019年10月20日,第六届世界互联网大会发布了15项“世界互联网领先科技成果”,其中有5项成果均属于芯片领域,分别为华为高性能服务器芯片“鲲鹏920”、清华大学“面向通用人工智能的异构融合天机芯片”、“特斯拉全自动驾驶芯片”、寒武纪云端AI芯片、“思元270”、赛灵思“Versal自适应计算加速平台”.现有3名学生从这15项“世界互联网领先科技成果”中分别任选1项进行了解,且学生之间的选择互不影响,则至少有1名学生选择“芯片领域”的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆柱内有一个三棱锥![]() ,
,![]() 为圆柱的一条母线,
为圆柱的一条母线,![]() ,
,![]() 为下底面圆
为下底面圆![]() 的直径,
的直径,![]() ,
,![]() .
.

(1)在圆柱的上底面圆内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
(2)设点![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,AB是圆O:x2+y2=1的直径,且点A在第一象限;圆O1:(x﹣a)2+y2=r2(a>0)与圆O外离,线段AO1与圆O1交于点M,线段BM与圆O交于点N,且![]() ,则a的取值范围为_______.
,则a的取值范围为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,AD=AP=3,点M是棱PD的中点.
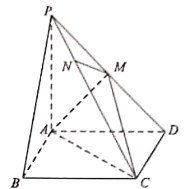
(1)求二面角M—AC—D的余弦值;
(2)点N是棱PC上的点,已知直线MN与平面ABCD所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比q>1,且a3+a4+a5=28,a4+2是a3,a5的等差中项.数列{bn}满足b1=1,数列{(bn+1﹣bn)an}的前n项和为2n2+n.
(1)求数列{an}的通项公式;
(2)求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 过点
过点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,设直线![]() 与圆
与圆![]() 相切与点
相切与点![]() ,与椭圆
,与椭圆![]() 相切于点
相切于点![]() ,当
,当![]() 为何值时,线段
为何值时,线段![]() 长度最大?并求出最大值.
长度最大?并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com