
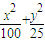 =1£¬n=3£®µćP1£Ø3£¬0£©¼°S3=255£¬ĒóµćP3µÄ×ų±ź£»£ØÖ»ŠčŠ“³öŅ»øö£©
=1£¬n=3£®µćP1£Ø3£¬0£©¼°S3=255£¬ĒóµćP3µÄ×ų±ź£»£ØÖ»ŠčŠ“³öŅ»øö£© £Øa£¾b£¾0£©£®µćP1£Øa£¬0£©£¬¶ŌÓŚøų¶ØµÄ×ŌČ»Źżn£¬µ±¹«²īd±ä»ÆŹ±£¬ĒóSnµÄ×īŠ”Öµ£»
£Øa£¾b£¾0£©£®µćP1£Øa£¬0£©£¬¶ŌÓŚøų¶ØµÄ×ŌČ»Źżn£¬µ±¹«²īd±ä»ÆŹ±£¬ĒóSnµÄ×īŠ”Öµ£»
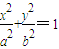 £Øa£¾b£¾0£©ÉĻø÷µćµÄ×īŠ”¾ąĄėĪŖb£¬×ī“ó¾ąĄėĪŖa£®øł¾Ża1=a2£¬ÅŠ¶Ļd£¼0£¬½ų¶ųøł¾Żan”Żb2£¬ĒóµĆ
£Øa£¾b£¾0£©ÉĻø÷µćµÄ×īŠ”¾ąĄėĪŖb£¬×ī“ó¾ąĄėĪŖa£®øł¾Ża1=a2£¬ÅŠ¶Ļd£¼0£¬½ų¶ųøł¾Żan”Żb2£¬ĒóµĆ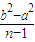 ”Üd£¬½ų¶ųÅŠ¶ĻSnŌŚ[
”Üd£¬½ų¶ųÅŠ¶ĻSnŌŚ[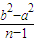 £¬0£©ÉĻµŻŌö£¬½ų¶ųĒóµĆSnµÄ×īŠ”Öµ£®
£¬0£©ÉĻµŻŌö£¬½ų¶ųĒóµĆSnµÄ×īŠ”Öµ£® £Øa1+a3£©=255£¬µĆa3=|OP3|3=70£®
£Øa1+a3£©=255£¬µĆa3=|OP3|3=70£®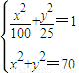 £¬µĆ
£¬µĆ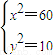 £¬
£¬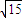 £¬
£¬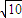 £©£®
£©£®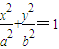 £Øa£¾b£¾0£©ÉĻø÷µćµÄ×īŠ”¾ąĄėĪŖb£¬×ī“ó¾ąĄėĪŖa£®
£Øa£¾b£¾0£©ÉĻø÷µćµÄ×īŠ”¾ąĄėĪŖb£¬×ī“ó¾ąĄėĪŖa£® ”Üd£¼0£®”ßn”Ż3£¬
”Üd£¼0£®”ßn”Ż3£¬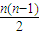 £¾0
£¾0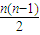 dŌŚ[
dŌŚ[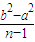 £¬0£©ÉĻµŻŌö£¬
£¬0£©ÉĻµŻŌö£¬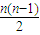 •
•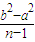 =
=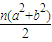 £®
£® -
-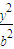 =1£¬µćP1£Øa£¬0£©£¬
=1£¬µćP1£Øa£¬0£©£¬

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 1 | 2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| x2 |
| 100 |
| y2 |
| 25 |
| x2 |
| a2 |
| y2 |
| b2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 2x | ||
2x+
|
| OP |
| 1 |
| 2 |
| OP1 |
| OP2 |
| 1 |
| 2 |
| n |
 |
| i=1 |
| i |
| n |
| 1 | ||||
(Sn+
|
| 2 |
| an |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| n |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| x2 |
| 9 |
| x2 |
| a2 |
| y2 |
| b2 |
| ·ūŗÅŅāŅå | ±¾ŹŌ¾ķĖłÓĆ·ūŗÅ | µČĶ¬ÓŚ”¶ŹµŃé½Ģ²Ä”··ūŗÅ | ||||
| ĻņĮæ×ų±ź |
|
| ||||
| ÕżĒŠ | tg | tan |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| a•2x | ||
2x+
|
| 2 |
| OP |
| 1 |
| 2 |
| OP1 |
| OP2 |
| 1 |
| 2 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com