

思路分析:本题首先要建立适当直角坐标系,动点P满足的条件(等量关系)题设中没有明显给出,要从题意中分析找出等量关系.连结PB,则|PM|=|PB|,由此|PA|+|PB|=|PA|+|PM|=|AM|=4,即动点P到两定点A,B距离之和为常数.
解:以过A,B两点的直线为x轴,A,B两点的中点O为坐标原点,建立直角坐标系.
∵|AB|=2,∴A,B两点坐标分别为(-1,0),(1,0).
连结PB.∵l垂直平分线段BM,
∴|PM|=|PB|,
|PA|+|PB|=|PA|+|PM|=|AM|=4.
设点P(x,y),由两点距离公式得
![]() =4.
=4.
化简方程,移项两边平方得(移项)
![]() =4-x,
=4-x,
两边再平方移项,得![]() =1,即为所求点P轨迹方程.
=1,即为所求点P轨迹方程.
方法归纳 通过分析题意利用几何图形的有关性质,找出P点与两定点A,B距离之和为常数4,是解本题的关键.方程化简过程也是很重要的,且化简过程也保证了等价性.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
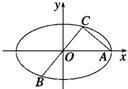 如图所示,已知A,B,C是椭圆E:
如图所示,已知A,B,C是椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| PQ |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
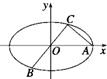 如图所示,已知A、B、C是椭圆E:
如图所示,已知A、B、C是椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
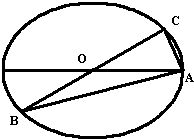 如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且| AC |
| BC |
| PQ |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
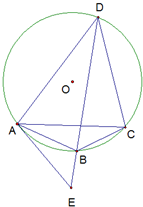 如图所示,已知A,B,C是圆O上三个点,AB弧等于BC弧,D为弧AC上一点,过点A做圆O的切线交BD延长线于E
如图所示,已知A,B,C是圆O上三个点,AB弧等于BC弧,D为弧AC上一点,过点A做圆O的切线交BD延长线于E| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知A、B、C是椭圆E:![]() =1(a>b>0)上的三点,其中点
=1(a>b>0)上的三点,其中点
A的坐标为(2![]() ,0),BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.
,0),BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.
(1)求点C的坐标及椭圆E的方程;
(2)若椭圆E上存在两点P、Q,使得∠PCQ的平分线总是垂直于x轴,试判断向量![]() 与
与![]() 是否共线,并给出证明.
是否共线,并给出证明. 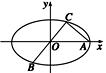
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com