
【题目】已知函数![]() ,其中
,其中![]() 是
是![]() 的导函数.
的导函数.
若![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)求证:![]() ,其中n∈N*.
,其中n∈N*.
科目:高中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯,由此催生了一批外卖点餐平台。已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:

以这80名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率。
(1)若某送餐员一天送餐的总距离为120千米,试估计该送餐员一天的送餐份数;(四舍五入精确到整数)
(2)若该外卖平台给送餐员的送餐费用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份5元,超过4千米为远距离,每份10元。
(i)记X为送餐员送一份外卖的收入(单位:元),求X的分布列和数学期望;
(ii)若送餐员一天的目标收入不低于180元,试估计一天至少要送多少份外卖?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为正数,给出下列命题:
①若a2﹣b2=1,则a﹣b<1;
②若![]() =1,则a﹣b<1;
=1,则a﹣b<1;
③ea﹣eb=1,则a﹣b<1;
④若lna﹣lnb=1,则a﹣b<1.
其中真命题的有_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣alnx+(a+1)x﹣![]() (a>0).
(a>0).
(1)讨论函数f(x)的单调性;
(2)若f(x)≥﹣![]() +ax+b恒成立,求a
+ax+b恒成立,求a![]() 时,实数b的最大值.
时,实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)
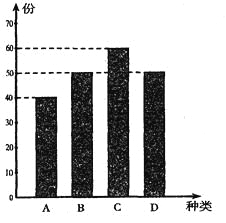
某学校餐厅新推出![]() 、
、![]() 、
、![]() 、
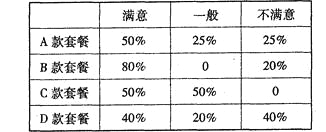
、![]() 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20分进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20分进行统计,统计结果如下面表格所示:
(1) 若同学甲选择的是![]() 款套餐,求甲的调查问卷被选中的概率;
款套餐,求甲的调查问卷被选中的概率;
(2) 若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这2人中至少有一人选择的是![]() 款套餐的概率。
款套餐的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当时
的图象.当时![]() ,求函数
,求函数![]() 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com