
【题目】若![]() 是一个由数字1,2,3,4,5,6,7,8,9组成的
是一个由数字1,2,3,4,5,6,7,8,9组成的![]() 位正整数,并同时满足如下两个条件:
位正整数,并同时满足如下两个条件:
(1)数字1,2,…,![]() 在
在![]() 中各出现两次;
中各出现两次;
(2)每两个相同的数字![]() 之间恰有
之间恰有![]() 个数字.
个数字.
此时,我们称这样的正整数![]() 为“好数”.例如,当
为“好数”.例如,当![]() 时,
时,![]() 可以是312 132.试确定满足条件的正整数
可以是312 132.试确定满足条件的正整数![]() 的值,并各写出一个相应的好数
的值,并各写出一个相应的好数![]() .
.
 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】已知关于![]() 的一元二次函数
的一元二次函数![]() ,从集合
,从集合![]() 中随机取一个数作为此函数的二次项系数
中随机取一个数作为此函数的二次项系数![]() ,从集合
,从集合![]() 中随机取一个数作为此函数的一次项系数
中随机取一个数作为此函数的一次项系数![]() .
.
(1)若![]() ,
,![]() ,求函数
,求函数![]() 有零点的概率;
有零点的概率;
(2)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙两个企业的用电负荷量![]() 关于投产持续时间
关于投产持续时间![]() (单位:小时)的关系
(单位:小时)的关系![]() 均近似地满足函数
均近似地满足函数![]() .
.
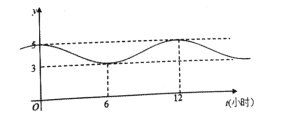
(1)根据图象,求函数![]() 的解析式;
的解析式;
(2)为使任意时刻两企业用电负荷量之和不超过9,现采用错峰用电的方式,让企业乙比企业甲推迟![]() 小时投产,求
小时投产,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1,2,3,4的四张卡片,现从甲、乙两个盒子中各取出一张卡片,每张卡片被取出的可能性相等.
(1)求取出的两张卡片上标号为相邻整数的概率;
(2)求取出的两张卡片上标号之和能被3整除的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将某校高二年级某班的学业水平测试数学成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五组,绘制而成的茎叶图、频率分布直方图如下,由于工作疏忽,茎叶图有部分被损坏,频率分布直方图也不完整,请据此解答如下问题:(注:该班同学数学成绩均在区间
五组,绘制而成的茎叶图、频率分布直方图如下,由于工作疏忽,茎叶图有部分被损坏,频率分布直方图也不完整,请据此解答如下问题:(注:该班同学数学成绩均在区间![]() 内)
内)

(1)将频率分布直方图补充完整.
(2)该班希望组建两个数学学习互助小组,班上数学成绩最好的两位同学分别担任两组组长,将此次成绩低于60分的同学作为组员平均分到两组,即每组有一名组长和两名成绩低60分的组员,求此次考试成绩为52分、54分和98分的三名同学分到同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,在
,在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,总有
怎样变化,总有![]() 为直角?若存在,求出点
为直角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱台![]() 中,
中,![]() 平面ABCD,四边形ABCD为平行四边形,
平面ABCD,四边形ABCD为平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() ,E为DC中点.
,E为DC中点.
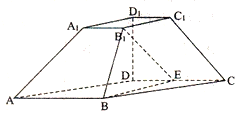
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求三棱锥![]() 的高.
的高.
(注:棱台的两底面相似)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com