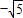(1)将分别写有1,2,3,4,5,6,7的7张卡片随机排成一排,则其中的奇数卡片都相邻或偶数卡片都相邻的概率是 .
(2)点P(3,m)到圆x2-2x+y2=0上的点的最短距离为2,并且点P在不等式3x+2y-5<0表示的平面区域内,则m= .
【答案】
分析:(1)利用排列方法求出7张卡片随机排成一排所有的排法,再利用间接法求出奇数卡片都相邻或偶数卡片都相邻的所有的排法,利用古典概型概率公式求出概率.
(2)求出p到圆的圆心的距离再减去半径得到点P(3,m)到圆x
2-2x+y
2=0上的点的最短距离,利用不等式表示平面区间满足的条件得到m满足的不等关系,求出m的值.
解答:解:(1)1,2,3,4,5,6,7的7张卡片随机排成一排,所有的排法有A
77=5040
其中的奇数卡片都相邻或偶数卡片都相邻的排法有A
44•A
44+A
33•A
55-2A
44•A
33=1008
∴其中的奇数卡片都相邻或偶数卡片都相邻的概率是
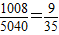
(2)点P(3,m)到圆x
2-2x+y
2=0上的点的最短距离为
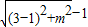
∴
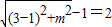
①
又P在不等式3x+2y-5<0表示的平面区域内
∴9+2m-5<0②
解①②得
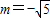
故答案为
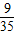
;
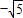 点评:
点评:求古典概型的事件的概率.应该先求出各个事件包含的基本事件的个数,求基本事件个数的常用方法有:列举法、排列、组合法、图表法.

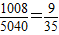
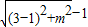
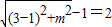 ①
①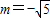
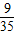 ;
;