
【题目】已知函数![]() 且a≠0).
且a≠0).
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)的极小值为![]() ,试求a的值.
,试求a的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可知![]() .
.![]() ,由此能求出曲线y=f(x)在点(1,f(1))处的切线方程.
,由此能求出曲线y=f(x)在点(1,f(1))处的切线方程.
(2)当a<-1时,求出![]() ,解得
,解得![]() ,不成立;②当a=-1时,
,不成立;②当a=-1时,![]() ≤0在(0,+∞)上恒成立,f(x)在(0,+∞)单调递减.f(x)无极小值;当-1<a<0时,极小值f(1)=-a-4,由题意可得
≤0在(0,+∞)上恒成立,f(x)在(0,+∞)单调递减.f(x)无极小值;当-1<a<0时,极小值f(1)=-a-4,由题意可得![]() ,求出
,求出![]() ;当a>0时,极小值f(1)=-a-4.由此能求出a的值.
;当a>0时,极小值f(1)=-a-4.由此能求出a的值.
(1)函数f(x)=(2ax2+4x)lnx-ax2-4x(a∈R,且a≠0).
由题意可知![]() .
.![]()
∴曲线y=f(x)在点(1,f(1))处的切线方程为![]() .
.
(Ⅱ)①当a<-1时,x变化时![]() 变化情况如下表:
变化情况如下表:
x |
|
|
| 1 | (1,+∞) |
| - | 0 | + | 0 | - |
f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
此时![]() ,解得
,解得![]() ,故不成立.
,故不成立.
②当a=-1时,![]() ≤0在(0,+∞)上恒成立,所以f(x)在(0,+∞)单调递减.
≤0在(0,+∞)上恒成立,所以f(x)在(0,+∞)单调递减.
此时f(x)无极小值,故不成立.
③当-1<a<0时,x变化时![]() 变化情况如下表:
变化情况如下表:
x | (0,1) | 1 |
|
|
|
| - | 0 | + | 0 | - |
f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
此时极小值f(1)=-a-4,由题意可得![]() ,
,
解得![]() 或
或![]() .
.
因为-1<a<0,所以![]() .
.
④当a>0时,x变化时![]() 变化情况如下表:
变化情况如下表:
x | (0,1) | 1 | (1,+∞) |
| - | 0 | + |
f(x) | ↘ | 极小值 | ↗ |
此时极小值f(1)=-a-4,由题意可得![]() ,
,
解得![]() 或
或![]() ,故不成立.
,故不成立.
综上所述![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
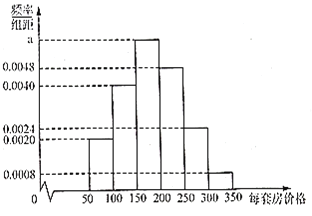
【题目】某房产销售公司从登记购房的客户中随机选取了50名客户进行调查,按他们购一套房的价格(万元)分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 得到频率分布直方图如图所示.用频率估计概率.
得到频率分布直方图如图所示.用频率估计概率.
房产销售公司每卖出一套房,房地产商给销售公司的佣金如下表(单位:万元):
房价区间 |
|
|
|
|
|
|
佣金收入 | 1 | 2 | 3 | 4 | 5 | 6 |
(1)求![]() 的值;
的值;
(2)求房产销售公司卖出一套房的平均佣金;
(3)若该销售公司平均每天销售4套房,请估计公司月(按30天计)利润(利润=总佣金-销售成本).
该房产销售公司每月(按30天计)的销售成本占总佣金的百分比按下表分段累计/span>计算:
月总佣金 | 不超过100万元的部分 | 超过100万元至200万元的部分 | 超过200万元至300万元的部分 | 超过300万元的部分 |
销售成本占 佣金比例 |
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是一个三棱锥,
是一个三棱锥,![]() 是圆的直径,
是圆的直径,![]() 是圆上的点,
是圆上的点,![]() 垂直圆所在的平面,
垂直圆所在的平面,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点.
的中点.
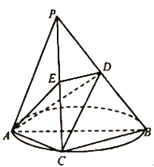
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 是
是![]() ,
,![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一件刚出土的珍贵文物要在博物馆大厅中央展出,需要设计各面是玻璃平面的无底正四棱柱将其罩住,罩内充满保护文物的无色气体.已知文物近似于塔形,高1.8米,体积0.5立方米,其底部是直径为0.9米的圆形,要求文物底部与玻璃罩底边至少间隔0.3米,文物顶部与玻璃罩上底面至少间隔0.2米,气体每立方米1000元,则气体费用最少为( )元

A.4500B.4000C.2880D.2380
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程,持有旅游年卡一年内可不限次畅游全市19家签约景区.为了解市民每年旅游消费支出情况![]() 单位:百元
单位:百元![]() ,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
组别 |
|
|
|
|
|
频数 | 10 | 390 | 400 | 188 | 12 |
![]() 求所得样本的中位数
求所得样本的中位数![]() 精确到百元
精确到百元![]() ;
;
![]() 根据样本数据,可近似地认为市民的旅游费用支出服从正态分布
根据样本数据,可近似地认为市民的旅游费用支出服从正态分布![]() ,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
![]() 若年旅游消费支出在
若年旅游消费支出在![]() 百元
百元![]() 以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
![]() 参考数据:
参考数据:![]() ,
,![]() ;
;![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com