
【题目】已知椭圆C:![]()
![]() 的焦距为
的焦距为![]() ,短半轴的长为2,过点P(-2,1)且斜率为1的直线l与椭圆C交于A,B两点.
,短半轴的长为2,过点P(-2,1)且斜率为1的直线l与椭圆C交于A,B两点.
(1)求椭圆C的方程;
(2)求弦AB的长.
科目:高中数学 来源: 题型:
【题目】如图所示:在五面体ABCDEF中,四边形EDCF是正方形,AD=DE=1,∠ADE=90°,∠ADC=∠DCB=120°.
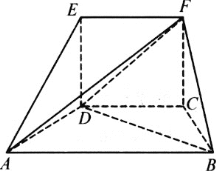
(Ⅰ)求证:平面ABCD⊥平面EDCF;
(Ⅱ)求三棱锥A-BDF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点F,直线y=4与y轴的交点为P,与抛物线C的交点为Q,且|QF|=2|PQ|.
(1)求p的值;
(2)已知点T(t,-2)为C上一点,M,N是C上异于点T的两点,且满足直线TM和直线TN的斜率之和为![]() ,证明直线MN恒过定点,并求出定点的坐标.
,证明直线MN恒过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴为正半轴为极轴建立极坐标系.已知曲线
轴为正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 过定点
过定点![]() 且倾斜角为
且倾斜角为![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)把曲线![]() 化成直角坐标方程,并求
化成直角坐标方程,并求![]() 的值;
的值;
(2)若![]() 成等比数列,求直线
成等比数列,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1:![]() y2=1的左右顶点是双曲线C2:
y2=1的左右顶点是双曲线C2:![]() 的顶点,且椭圆C1的上顶点到双曲线C2的渐近线的距离为
的顶点,且椭圆C1的上顶点到双曲线C2的渐近线的距离为![]() .
.
(1)求双曲线C2的方程;
(2)若直线与C1相交于M1,M2两点,与C2相交于Q1,Q2两点,且![]()
![]() 5,求|M1M2|的取值范围.
5,求|M1M2|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除
给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,两条平行线
,两条平行线![]() 与
与![]() 间的距离为h,直线
间的距离为h,直线![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则该羡除的体积为
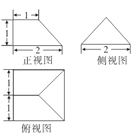
,则该羡除的体积为![]() 已知某羡除的三视图如图所示,则该羡除的体积为
已知某羡除的三视图如图所示,则该羡除的体积为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设点![]() ,
,![]() ,
,![]() (其中
(其中![]() 表示a、b中的较大数)为
表示a、b中的较大数)为![]() 、
、![]() 两点的“切比雪夫距离”.
两点的“切比雪夫距离”.
(1)若![]() ,Q为直线
,Q为直线![]() 上动点,求P、Q两点“切比雪夫距离”的最小值;
上动点,求P、Q两点“切比雪夫距离”的最小值;
(2)定点![]() ,动点
,动点![]() 满足
满足![]()
![]() ,请求出P点所在的曲线所围成图形的面积.
,请求出P点所在的曲线所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com