某市2008年11月份曾发生流感,据统计,11月1日该市流感病毒新感染者有20人,此后,每天的新感染者平均比前一天的新感染者增加50人,由于该市医疗部门采取措施,使该种病毒的传播得到控制,从某天起,每天的新感染者平均比前一天的新感染者减少30人,到11月30日为止,该市在这30日内该病毒新感染者共有8 670人,问11月几日,该市新感染此病毒的人数最多?并求这一天的新感染人数.
【答案】
分析:由题意知前n天流感病毒新感染者的人数,构成一个首项为20,公差为50的等差数列,写出一个感染的总人数,而后30-n天的流感病毒新感染者的人数,构成一个首项为50n-60,公差为-30,项数为30-n的等差数列,写出感染的总人数,根据数列的函数特性求出所求.
解答:解:设第n天新感染人数最多,则从第n+1天起该市医疗部门采取措施,
于是,前n天流感病毒新感染者的人数,构成一个首项为20,公差为50的等差数列,
其前n项和S
n=20n+
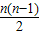
×50=25n
2-5n(1≤n<30,n∈N),
而后30-n天的流感病毒新感染者的人数,
构成一个首项为20+(n-1)×50-30=50n-60,公差为-30,项数为30-n的等差数列,
其前30-n项的和T
30-n=(30-n)(50n-60)+
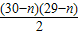
×(-30)=-65n
2+2445n-14850,
依题设构建方程有,S
n+T
30-n=8670,∴25n
2-5n+(-65n
2+2445n-14850)=8670,
化简得n
2-61n+588=0,∴n=12或n=49(舍去),第12天的新感染人数为20+(12-1)•50=570人.
故11月12日,该市新感染此病毒的人数最多,新感染人数为570人.
点评:解数学问题应用题重点在过好三关:(1)事理关:阅读理解,知道命题所表达的内容;(2)文理关:将“问题情景”中的文字语言转化为符号语言,用数学关系式表述事件;(3)数理关:由题意建立相关的数学模型,将实际问题数学化,并解答这一数学模型,得出符合实际意义的解答.

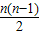 ×50=25n2-5n(1≤n<30,n∈N),
×50=25n2-5n(1≤n<30,n∈N),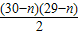 ×(-30)=-65n2+2445n-14850,
×(-30)=-65n2+2445n-14850,

 阅读快车系列答案
阅读快车系列答案