【题目】等腰三角形的周长是18，底边长y是一腰长x的函数，则（ ）
A.y＝9－x（0＜x≤9）
B.y＝9－x（0＜x＜9）
C.y＝18－2x（4．5≤x≤9）
D.y＝18－2x（4．5＜x＜9）
科目：高中数学 来源： 题型：
【题目】某单位共有10名员工，他们某年的收入如下表：
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪（万元） | 3 | 3.5 | 4 | 5 | 5.5 | 6.5 | 7 | 7.5 | 8 | 50 |
（1）从该单位中任取2人，此2人中年薪收入高于5万的人数记为
，求
的分布列和期望；
（2）已知员工年薪收入
与工作所限
成正相关关系，某员工工作第一年至第四年的年薪如下表：
工作年限 | 1 | 2 | 3 | 4 |
年薪（万元） | 3.0 | 4.2 | 5.6 | 7.2 |
预测该员工第五年的年薪为多少？
附：线性回归方程
中系数计算公式和参考数据分别为：
，
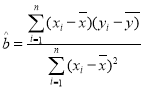，其中
为样本均值，
，
，（
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设a1，d为实数，首项为a1，公差为d的等差数列{an}的前n项和为Sn，满足S5S6＋15＝0．
（1）若S5＝5，求S6及a1；
（2）求d的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若函数
满足：
，则称为“
函数”．
（1）试判断
是否为“函数”，并说明理由；
（2）若为“函数”且
，
（ⅰ）求证：的零点在
上；
（ii）求证：对任意
，存在
，使
在
上恒成立．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地空气中出现污染，须喷洒一定量的去污剂进行处理.据测算，每喷洒
个单位的去污剂，空气中释放的浓度
（单位：毫克/立方米）随着时间
单位：天）变化的函数关系式，近似为
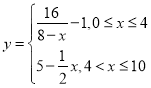,若多次喷洒，则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和. 由实验知，当空气中去污剂的浓度不低于
（毫克/立方米）时，它才能起到去污作用.
（1）若一次喷洒
个单位的去污剂，则去污时间可达几天？
（2）若第一次喷洒
个单位的去污剂，
天后再唢洒
个单位的去污剂，要使接来的
天中能够持续有效去污，试求
的最小值（精确到
，参考数据:
取
）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某化工厂近期要生产一批化工试剂，经市场调査得知，生产这批试剂厂家的生产成本有以下三个部分：①生产
单位试剂需要原料费
元; ②支付所有职工的工资总额由
元的基本工资和每生产单位试剂补貼所有职工
元组成; ③后续保养的平均费用是每单位
元（试剂的总产量为
单位,
）.
（1）把生产每单位试剂的成本表示为的函数关系
,并求出的最小值;
（2）如果产品全部卖出,据测算销售額
（元）关于产量
（单位）的函数关系为
,试问：当产量为多少时生产这批试剂的利润最高?
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】直线l交抛物线y2=2x于A、B两点，且OA⊥OB，则直线l过定点（ ）
A. （1，0） B. （2，0） C. （3，0） D. （4，0）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
