
【题目】设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使| A1B1|=| A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A. (![]() ,2] B. [
,2] B. [![]() ,2) C. (
,2) C. (![]() ,+
,+![]() ) D. [
) D. [![]() ,+
,+![]() )
)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知实数a、m满足a= ![]() cosxdx,(x+a+m)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7 , 且(a0+a2+a4+a6)2﹣(a1+a3+a5+a7)2=37 , 则m=( )
cosxdx,(x+a+m)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7 , 且(a0+a2+a4+a6)2﹣(a1+a3+a5+a7)2=37 , 则m=( )
A.﹣1或3
B.1或﹣3
C.1
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设实数x,y满足不等式组  ,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
A.(0,1)
B.(0,1]
C.(﹣∞,﹣2)
D.(﹣∞,﹣2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种出口产品的关税税率![]() ,市场价格
,市场价格![]() (单位:千元)与市场供应量
(单位:千元)与市场供应量![]() (单位:万件)之间近似满足关系式:
(单位:万件)之间近似满足关系式:![]() ,其中
,其中![]() 、
、![]() 均为常数.当关税税率为
均为常数.当关税税率为![]() 时,若市场价格为5千元,则市场供应量约为1万件;当关税税率为
时,若市场价格为5千元,则市场供应量约为1万件;当关税税率为![]() 时,若市场价格为7千元,则市场供应量约为2万件.
时,若市场价格为7千元,则市场供应量约为2万件.
(1)试确定![]() 、
、![]() 的值;
的值;
(2)市场需求量![]() (单位:万件)与市场价格
(单位:万件)与市场价格![]() 近似满足关系式:
近似满足关系式:![]() .当
.当![]() 时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率的最大值.
时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,已知点A(-2,0),直角顶点B(0,-2![]() ),点C在x轴上。
),点C在x轴上。
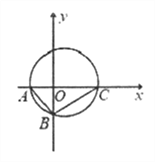
(1)求Rt△ABC外接圆的方程;
(2)求过点(-4,0)且与Rt△ABC外接圆相切的直线的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=﹣1,|an﹣an﹣1|=2n﹣1(n∈N,n≥2),且{a2n﹣1}是递减数列,{a2n}是递增数列,则a2016= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com