
 ,w=
,w= ,4≤v≤20,30≤w≤100.
,4≤v≤20,30≤w≤100. ≤y≤
≤y≤ .
.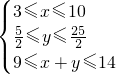 ;
;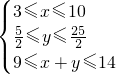 是图中阴影部分(包括边界).
是图中阴影部分(包括边界).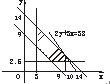
 的直线3x+2y=k中,
的直线3x+2y=k中,

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 某人上午7时,乘摩托艇以匀速v海里/时(4≤v≤20)从A港出发到距50海里的B港去,然后乘汽车以w千米/时(30≤w≤100)自B港向距300千米的C市驶去,应该在同一天下午4至9时到达C市.设汽车、摩托艇所需的时间分别是x,y小时.
某人上午7时,乘摩托艇以匀速v海里/时(4≤v≤20)从A港出发到距50海里的B港去,然后乘汽车以w千米/时(30≤w≤100)自B港向距300千米的C市驶去,应该在同一天下午4至9时到达C市.设汽车、摩托艇所需的时间分别是x,y小时.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省安庆市望江四中高三(上)第四次月考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com