练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】袋中装有除颜色外完全相同的黑球和白球共7个，其中白球3个，现有甲、乙两人从袋中轮流摸球，甲先取，乙后取，然后甲再取，…，取后不放回，直到两人中有一人取到白球时终止.每个球在每一次被取出的机会是等可能的.

    （1）求取球2次即终止的概率；

    （2）求甲取到白球的概率.

    【答案】（1）；（2）

    【解析】

    （1）第二次终止即：第一次摸到黑球第二次摸到白球；

    （2）根据规则，甲取到白球必须可能是第1,3,5次出现白球，且在摸到白球之前乙摸到黑球，结合树状图求解.

    （1）设事件A为“取球2次即终止”.即甲第一次取到的是黑球而乙取到的是白球，借助树状图求出相应事件的样本点数：

    因此，.

    （2）设事件B为“甲取到白球”，“第i次取到白球”为事件，因为甲先取，所以甲只可能在第1次，第3次和第5次取到白球.借助树状图求出相应事件的样本点数：

    所以

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥的底面是等腰梯形，，，，，.

    (1)证明:平面平面；

    (2)点E是棱PC上一点，且平面，求二面角的正弦值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中，已知M，N分别为线段BB1，A1C的中点，MN⊥AA1，且MA1＝MC.求证：

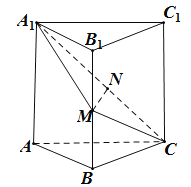
    （1）MN平面ABC；

    （2）平面A1MC⊥平面A1ACC1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB是圆O的直径，点C是圆O上异于A，B的点，PO垂直于圆O所在的平面，且PO＝OB＝1.

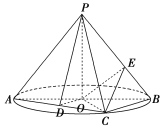
    (1)若D为线段AC的中点，求证：AC⊥平面PDO；

    (2)求三棱锥P－ABC体积的最大值；

    (3)若，点E在线段PB上，求CE＋OE的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4—4：坐标系与参数方程

    在直角坐标系xOy中，设倾斜角为α的直线l：（t为参数）与曲线C：（θ为参数）相交于不同的两点A，B．

    （Ⅰ）若α＝，求线段AB中点M的坐标；

    （Ⅱ）若｜PA｜·｜PB｜＝｜OP｜，其中P（2，），求直线l的斜率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列是公差为2的等差数列，且成等比数列．数列满足：，.

    （Ⅰ）求数列，的通项公式；

    （Ⅱ）设数列的前n项和为，且，若对，恒成立，求正整数k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：，；命题q：方程表示双曲线．

    ⑴若命题p为真命题，求实数m的取值范围；

    ⑵若命题“”为真命题，“”为假命题，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在△ABC中，∠B＝90°，AB＝BC＝2，P为AB边上一动点，PD∥BC交AC于点D，现将△PDA沿PD翻折至△PDA1，E是A1C的中点．

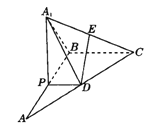
    （1）若P为AB的中点证明：DE∥平面PBA1．

    （2）若平面PDA1⊥平面PDA，且DE⊥平面CBA1，求二面角P﹣A1D﹣C的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）讨论函数的单调性；

    （2）若函数恰好有2个零点，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案