
【题目】已知椭圆![]() :
:![]() 的两个焦点与短轴的一个端点恰好围成一个面积为
的两个焦点与短轴的一个端点恰好围成一个面积为![]() 的等边三角形.
的等边三角形.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() 、
、![]() ,右焦点为
,右焦点为![]() ,
,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的动点,直线
的动点,直线![]() 与椭圆
与椭圆![]() 在点
在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 运动时,试判断以
运动时,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
【答案】(1)![]() ;(2)相切,证明见解析
;(2)相切,证明见解析
【解析】
(1)由条件可知,![]() ,解得
,解得![]() ,再根据条件求
,再根据条件求![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,表示点
,与椭圆方程联立,表示点![]() 的坐标,并表示直线
的坐标,并表示直线![]() 的方程,利用两直线的交点求点
的方程,利用两直线的交点求点![]() 的坐标,并表示圆心,利用圆心到直线的距离,判断直线与圆的位置关系.
的坐标,并表示圆心,利用圆心到直线的距离,判断直线与圆的位置关系.
解:(1)设椭圆半焦距为![]() ,
,
依题意有![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,故
,故![]() 的方程为
的方程为![]() .
.
(2)以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切,
相切,
证明如下:易知![]() ,
,![]() ,
,![]() ,在点
,在点![]() 处的切线方程为
处的切线方程为![]() .
.
由题意可设直线![]() 的方程为
的方程为![]() .
.
则点![]() 坐标为
坐标为![]() ,
,![]() 中点
中点![]() 的坐标为
的坐标为![]() .
.
由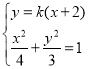 得
得![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
所以![]() ,
,![]() .
.
①当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
直线![]() 轴,此时以
轴,此时以![]() 为直径的圆
为直径的圆![]() 与直线
与直线![]() 相切.
相切.
②当![]() 时,则直线
时,则直线![]() 的斜率
的斜率![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
点![]() 到直线
到直线![]() 的距离
的距离
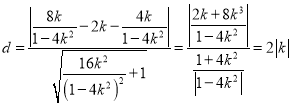 .
.
又因为![]() ,故以
,故以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
综上得,当直线![]() 绕点
绕点![]() 转动时,以
转动时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的年收益![]() 与投资额
与投资额![]() 成正比,其关系如图1;投资股票等风险型产品的年收益
成正比,其关系如图1;投资股票等风险型产品的年收益![]() 与投资额
与投资额![]() 的算术平方根成正比,其关系如图2.
的算术平方根成正比,其关系如图2.

(1)分别写出两种产品的年收益![]() 和
和![]() 的函数关系式;
的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大年收益,其最大年收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,双曲线![]() (a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
(a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
A.若PQ⊥x轴,则△PQF2的周长为![]()
B.连PA交l于D,则必有QD//x轴
C.若PQ中点为M,则必有PQ⊥MF2
D.连PO交双曲线C右支于点N,则必有PQ//NF2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四名同学组成一个4![]() 100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是( )
100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,已知A,a,b,给出下列说法:
中,已知A,a,b,给出下列说法:
①若![]() ,则此三角形最多有一解;
,则此三角形最多有一解;
②若![]() ,且
,且![]() ,则此三角形为直角三角形,且
,则此三角形为直角三角形,且![]() ;
;
③当![]() ,且
,且![]() 时,此三角形有两解.
时,此三角形有两解.
其中正确说法的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com