
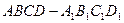 的棱长为2
的棱长为2 ,E为AB的中点.(Ⅰ)求证:
,E为AB的中点.(Ⅰ)求证: (Ⅱ)求异面直线BD1与CE所成角的余弦值;(Ⅲ)求点B到平面
(Ⅱ)求异面直线BD1与CE所成角的余弦值;(Ⅲ)求点B到平面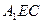 的距离.
的距离.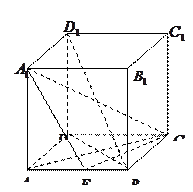
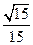 (Ⅲ)
(Ⅲ)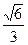
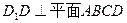
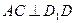 …………1分
…………1分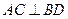 ……2分 ∵
……2分 ∵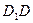 与
与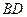 相交,∴
相交,∴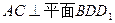 ……3分
……3分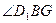 就是异面直线BD1与CE所成角…………………………5分
就是异面直线BD1与CE所成角…………………………5分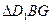 中,
中,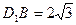
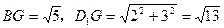 …………………6分
…………………6分
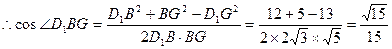
 异面直线
异面直线 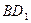 与CE所成角的余弦值是
与CE所成角的余弦值是 ………8分
………8分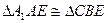
 ∴
∴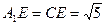 又∵
又∵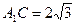 ∴ 点E到
∴ 点E到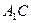 的距离
的距离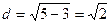 ,有:
,有: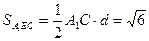
 ,…………11分
,…………11分 , 设点B到平面
, 设点B到平面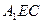 的距离为
的距离为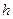 ,
,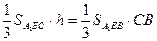 , 有
, 有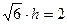 ,
,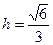 , 所以点B到平面
, 所以点B到平面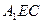 的距离为
的距离为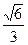 …14分
…14分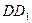 为
为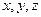 轴建立空间直角坐标系,则有B(2,2,0)、
轴建立空间直角坐标系,则有B(2,2,0)、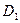 (0,0,2)、E(2,1,0)、C(0,2,0)、
(0,0,2)、E(2,1,0)、C(0,2,0)、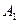 (2,0,2)∴
(2,0,2)∴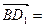 (-2,-2,2),
(-2,-2,2),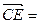 (2,-1,0)………5分
(2,-1,0)………5分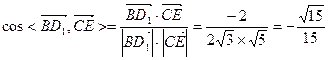 ……7分即余弦值是
……7分即余弦值是 8分
8分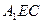 的法向量为
的法向量为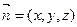 , 有:
, 有: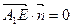 ,
,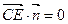 ,…8分
,…8分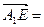 (0,1,-2),
(0,1,-2),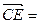 (2,-1,0)………9分
(2,-1,0)………9分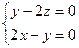
 ,令
,令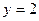 ,得
,得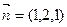 ………11分
………11分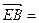 (0,1,0)有:点B到平面
(0,1,0)有:点B到平面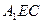 的距离为
的距离为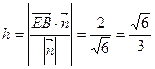 …14分
…14分

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源:不详 题型:解答题
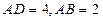 ,E、F分别是线段AB、BC的中点,
,E、F分别是线段AB、BC的中点,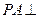 面ABCD. (1)
面ABCD. (1)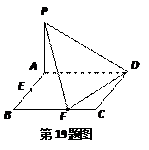 证明:PF⊥FD;
证明:PF⊥FD;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
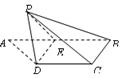
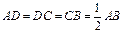 ,E是AB的中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角
,E是AB的中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角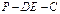 的大小为1200.
的大小为1200.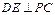 ;
;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
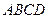 是直角梯形,
是直角梯形,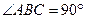 ,
,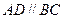 ,
,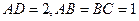 ,
,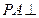 平面
平面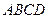 .
.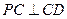 ;
;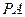 上是否存在一点
上是否存在一点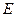 ,使得
,使得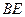 ∥平面
∥平面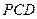 ?若存在,找出点
?若存在,找出点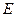 ,并证明:
,并证明: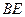 ∥平面
∥平面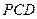 ;若不存在,请说明理由;
;若不存在,请说明理由;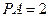 ,求二面角
,求二面角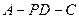 的余弦值.
的余弦值.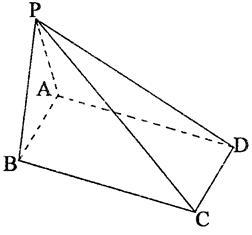
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
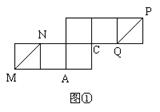
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.24 | B.36 | C.44 | D.56 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
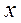 cm的内接圆柱.
cm的内接圆柱. 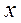 表示圆柱的侧面积;(2)当
表示圆柱的侧面积;(2)当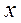 为何值时,圆柱的侧面积最大.
为何值时,圆柱的侧面积最大.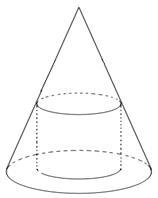 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com