
【题目】对于函数f(x)= ![]() ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N* , 且n≥2),令集合M={x|f2036(x)=x,x∈R},则集合M为( )
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N* , 且n≥2),令集合M={x|f2036(x)=x,x∈R},则集合M为( )
A.空集
B.实数集
C.单元素集
D.二元素集
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】已知互不重合的直线![]() ,互不重合的平面
,互不重合的平面![]() ,给出下列四个命题,正确命题的个数是
,给出下列四个命题,正确命题的个数是
①若![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,则
,则![]()
![]()
![]()
②若![]() ,
,![]() ,
,![]() 则
则![]()
③若![]() ,
,![]() ,
,![]() ,则
,则![]()
④若![]()
![]()
![]() ,
,![]()
![]()
![]() ,则
,则![]() //
//![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,离心率
,离心率![]() ,短轴长为2.
,短轴长为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点![]() 为椭圆上的一动点(非长轴端点),
为椭圆上的一动点(非长轴端点),![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,
点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,若
点,若![]() 面积为
面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]()
【解析】试题分析:(Ⅰ)由题意得![]() ,再由
,再由![]()
![]() 椭圆的方程为
椭圆的方程为![]() ;(Ⅱ)①当直线
;(Ⅱ)①当直线![]() 斜率不存在时,不妨取
斜率不存在时,不妨取![]() 面积为
面积为![]()
![]() ,不符合题意. ②当直线
,不符合题意. ②当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() , 由
, 由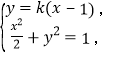
![]() 得
得![]()
![]()
![]()
![]() ,再求点
,再求点![]() 的直线
的直线![]() 的距离
的距离![]()
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]() 面积为
面积为![]()
![]()
![]()
![]() ∴
∴![]() 或
或![]()
![]() 所求方程为
所求方程为![]() 或
或![]() .
.
试题解析: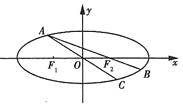
(Ⅰ)由题意得![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴椭圆的方程为![]() .
.
(Ⅱ)①当直线![]() 斜率不存在时,不妨取
斜率不存在时,不妨取![]() ,
,
∴![]() 面积为
面积为![]()
![]() ,不符合题意.
,不符合题意.
②当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() ,
,
由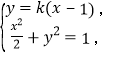 化简得
化简得![]() ,
,
设![]() ,
,
∴![]()
![]() ,
,
∵点![]() 的直线
的直线![]() 的距离
的距离![]() ,
,
又![]() 是线段
是线段![]() 的中点,∴点
的中点,∴点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴![]() 面积为
面积为![]()
![]()
![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 或
或![]() ,
,
∴直线![]() 的方程为
的方程为![]() 或
或![]() .
.
【题型】解答题
【结束】
25
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间与极值;
的单调区间与极值;
(Ⅱ)若![]() ,且
,且![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图放置的边长为2的正三角形ABC沿x轴滚动,记滚动过程中顶点A的横、纵坐标分别为![]() 和
和![]() ,且
,且![]() 是
是![]() 在映射
在映射![]() 作用下的象,则下列说法中:
作用下的象,则下列说法中:

① 映射![]() 的值域是
的值域是![]() ;
;
② 映射![]() 不是一个函数;
不是一个函数;
③ 映射![]() 是函数,且是偶函数;
是函数,且是偶函数;
④ 映射![]() 是函数,且单增区间为
是函数,且单增区间为![]() ,
,
其中正确说法的序号是___________.
说明:“正三角形ABC沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点B为中心顺时针旋转,当顶点C落在x轴上时,再以顶点C为中心顺时针旋转,如此继续.类似地,正三角形ABC可以沿x轴负方向滚动.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B均为锐角,则cosA>sinB是△ABC为钝角三角形的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
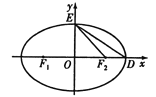
【题目】如图![]() 为椭圆C:
为椭圆C:![]()
![]() 的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率
的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率![]() ,
,![]() 的面积为
的面积为![]() .若点
.若点![]() 在椭圆C上,则点
在椭圆C上,则点![]() 称为点M的一个“椭圆”,直线
称为点M的一个“椭圆”,直线![]() 与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
(1)求椭圆C的标准方程;
(2)问是否存在过左焦点![]() 的直线
的直线![]() ,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com