
分析 (1)利用配方法得到圆的标准方程,根据直线垂直的条件:斜率之积为-1,点与圆的位置关系即可求出a的取值范围;
(2)利用PM=$\sqrt{3}$PN,可得圆的方程,结合两个圆相交,求实数a的取值范围.
解答 解:(1)圆的标准方程为(x+1)2+(y-2)2=5-a,
则圆心C(-1,2),半径r=$\sqrt{5-a}$,
∵弦AB的中点为M(0,1).
∴点M在圆内部,即$\sqrt{{1}^{2}+(1-2)^{2}}$<$\sqrt{5-a}$,
∴5-a>2,即a<3.
∵弦的中点为M(0,1).
∴直线CM的斜率k=$\frac{2-1}{-1-0}$=-1,
则直线l的斜率k=1,
则直线l的方程为y-1=x,即x-y+1=0.
(2)设P(x,y),由|PM|=$\sqrt{3}$|PN|,
可得$\sqrt{(x-0)^{2}+(y-1)^{2}}$=$\sqrt{3}$•$\sqrt{(x-0)^{2}+(y+3)^{2}}$,
化简可得,x2+(y+5)2=12,
即为P的轨迹为圆心(0,-5),半径为2$\sqrt{3}$的圆.
据题意:两个圆相交:|$\sqrt{5-a}$-2$\sqrt{3}$|<$\sqrt{1+(2+5)^{2}}$<$\sqrt{5-a}$+2$\sqrt{3}$,
解得-57-20$\sqrt{6}$<a<-57+20$\sqrt{6}$,且-57+20$\sqrt{6}$<3,
则实数a的取值范围是(-57-20$\sqrt{6}$,-57+20$\sqrt{6}$).
点评 本题主要考查直线和圆的方程的应用,同时考查点与圆及圆与圆的位置关系,利用配方法将圆配成标准方程是解决本题的关键.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
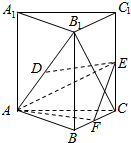 已知三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AB=AC,D,E,F分别为B1A,C1C,BC的中点.
已知三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AB=AC,D,E,F分别为B1A,C1C,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
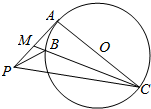 如右图所示,PA为圆O的切线,切点为A,AC是直径,M为PA的中点,MC与圆交于点B.
如右图所示,PA为圆O的切线,切点为A,AC是直径,M为PA的中点,MC与圆交于点B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.
如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com