
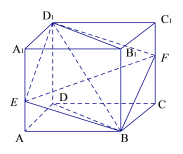
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点E,交棱
于点E,交棱![]() 于点F,则:
于点F,则:
①平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
②四边形![]() 一定是平行四边形;
一定是平行四边形;
③平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
④四边形![]() 的面积有最大值.
的面积有最大值.
其中所有正确结论的序号为( )
A.①④B.②③C.①②④D.①②③④
【答案】C
【解析】
根据正方体的性质对每个命题进行判断.结合排除法可选正确结论.
截面上方几何体分割成四棱锥四棱锥![]() ,四棱锥
,四棱锥![]() ,三棱锥
,三棱锥![]() ,截面下方几何体对称的也是三个棱锥,对应体积相等(特殊位置截面更容易得此结论),①正确,排除B;
,截面下方几何体对称的也是三个棱锥,对应体积相等(特殊位置截面更容易得此结论),①正确,排除B;
由正方体相对两个面平行,根据面面平行的性质定理知四边形![]() 的两组对边平行,从而是平行四边形,②正确,排除A;
的两组对边平行,从而是平行四边形,②正确,排除A;
当![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,这时可证
中点,这时可证![]() 平面
平面![]() (先证
(先证![]() ),从而平面
),从而平面![]() 与平面
与平面![]() 垂直,③错误,排除D,
垂直,③错误,排除D,
只有C可选了.
事实上,四边形![]() 即有最大值也有最小值.
即有最大值也有最小值.![]() 与
与![]() (或
(或![]() )重合时面积最大,
)重合时面积最大,![]() 是
是![]() 中点时,面积最小.
中点时,面积最小.
设![]() ,正方体棱长为1,
,正方体棱长为1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
所以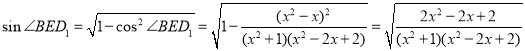 ,
,
所以![]()
![]() ,
,
所以![]() 或1时,
或1时,![]() 取得最大值
取得最大值![]() .④正确.
.④正确.
故选:C.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,底面ABCD是边长为3的正方形,平面ADEF⊥平面ABCD,AF∥DE,AD⊥DE,AF=![]() ,DE=
,DE=![]() .
.
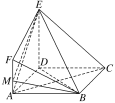
(1)求直线CA与平面BEF所成角的正弦值;
(2)在线段AF上是否存在点M,使得二面角MBED的大小为60°?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴的建立极坐标系,曲线
轴正半轴为极轴的建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若点![]() 与点
与点![]() 分别为曲线
分别为曲线![]() 动点,求
动点,求![]() 的最小值,并求此时的
的最小值,并求此时的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为3的正方体ABCD-A1B1C1D1中,A1E=CF=1.
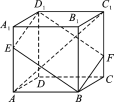
(1)求两条异面直线AC1与BE所成角的余弦值;
(2)求直线BB1与平面BED1F所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内.如图所示的小木块中,上面7层为高尔顿板,最下面一层为改造的高尔顿板,小球从通道口落下,第一次与第2层中间的小木块碰撞,以![]() 的概率向左或向右滚下,依次经过6次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以
的概率向左或向右滚下,依次经过6次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以![]() 的概率向左滚下,或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以
的概率向左滚下,或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以![]() 的概率向右滚下.
的概率向右滚下.

(1)若进行一次高尔顿板试验,求小球落入第7层第6个空隙处的概率;
(2)小明同学在研究了高尔顿板后,利用该图中的高尔顿板来到社团文化节上进行盈利性“抽奖”活动,8元可以玩一次高尔顿板游戏,小球掉入X号球槽得到的奖金为![]() 元,其中
元,其中![]() .
.
(i)求X的分布列:
(ii)高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小明同学能盈利吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com