
分析 对5个命题分别进行判断,即可得出结论.
解答 解:f(x)=ax-a-x,f(-x)=a-x-ax=-f(x),函数的奇函数,f(x)的图象关于原点对称,①正确;
f(x)=ax-a-x,当a>1时是增函数,当0<a<<A<1时是减函数,命题(2)错误;F(|X|)=F(|-X|),所以F(|X|)的图象关于Y轴对称,命题(3)正确;当0<A1时,函数f(x)是减函数,②不正确;
函数f(|x|)的图象关于y轴对称,③正确;
当0<a<1时,函数f(|x|)的最大值是0,④正确;
当a>1时,函数f(x)没有最大值,函数f(|x|)的最大值是0,⑤不正确.
故答案为:①③④.
点评 本题考查命题的真假判断,考查函数的性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [2kπ-$\frac{π}{4}$,2kπ+$\frac{π}{4}$](k∈Z) | B. | [kπ,kπ+$\frac{π}{4}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$](k∈Z) | D. | [kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
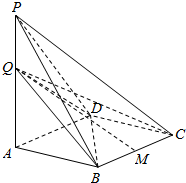 已知四棱锥P-ABCD中,底面ABCD为∠ABC=$\frac{2}{3}$π的菱形,PA⊥平面ABCD,点Q在直线PA上.
已知四棱锥P-ABCD中,底面ABCD为∠ABC=$\frac{2}{3}$π的菱形,PA⊥平面ABCD,点Q在直线PA上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com