
【题目】已知函数![]() 的图象在
的图象在![]() 处的切线与函数
处的切线与函数![]() 的图象在
的图象在![]() 处的切线互相平行.
处的切线互相平行.
(1)求![]() 的值;
的值;
(2)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.“![]() 为真”是“
为真”是“![]() 为真”的充分不必要条件;
为真”的充分不必要条件;
B.若数据![]() 的平均数为1,则
的平均数为1,则![]() 的平均数为2;
的平均数为2;
C.在区间![]() 上随机取一个数
上随机取一个数![]() ,则事件“
,则事件“![]() ”发生的概率为
”发生的概率为![]()
D.设从总体中抽取的样本为![]() 若记样本横、纵坐标的平均数分别为
若记样本横、纵坐标的平均数分别为![]() ,则回归直线
,则回归直线![]() 必过点
必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市房管局为了了解该市市民![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间买二手房情况,首先随机抽样其中
月期间买二手房情况,首先随机抽样其中![]() 名购房者,并对其购房面积
名购房者,并对其购房面积![]() (单位:平方米,
(单位:平方米,![]() )进行了一次调查统计,制成了如图
)进行了一次调查统计,制成了如图![]() 所示的频率分布直方图,接着调查了该市
所示的频率分布直方图,接着调查了该市![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间当月在售二手房均价
月期间当月在售二手房均价![]() (单位:万元/平方米),制成了如图
(单位:万元/平方米),制成了如图![]() 所示的散点图(图中月份代码
所示的散点图(图中月份代码![]() 分别对应
分别对应![]() 年
年![]() 月至
月至![]() 年
年![]() 月).
月).
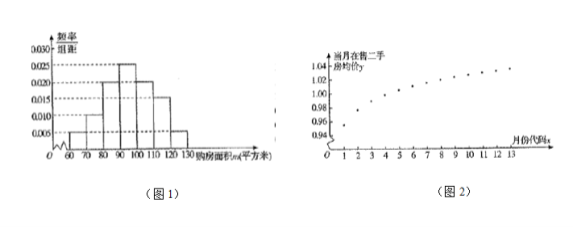
(1)试估计该市市民的购房面积的中位数![]() ;
;
(2)现采用分层抽样的方法从购房面积位于![]() 的
的![]() 位市民中随机抽取
位市民中随机抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,求这
人,求这![]() 人的购房面积恰好有一人在
人的购房面积恰好有一人在![]() 的概率;
的概率;
(3)根据散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值如下表所示:
,并得到一些统计量的值如下表所示:
|
| |
| 0.000591 | 0.000164 |
| 0.006050 | |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出![]() 年
年![]() 月份的二手房购房均价(精确到
月份的二手房购房均价(精确到![]() )
)
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(参考公式)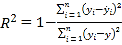
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进位制是人们为了计数和运算方便而约定的计数系统,“满几进一”就是几进制,不同进制之间可以相互转化,例如把十进制的89转化为二进制,根据二进制数“满二进一”的原则,可以用2连续去除89得商,然后取余数,具体计算方法如下:
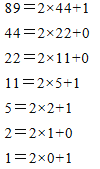
把以上各步所得余数从下到上排列,得到89=1011001(2)这种算法叫做“除二取余法”,上述方法也可以推广为把十进制数化为k进制数的方法,称为“除k取余法”,那么用“除k取余法”把89化为七进制数为_.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() 且满足
且满足![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(2)若方程![]() 有实数根
有实数根![]() ,则称
,则称![]() 为函数
为函数![]() 的一个不动点,设正数
的一个不动点,设正数![]() 为函数
为函数![]() 的一个不动点,且
的一个不动点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com