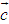已知函数f(x)=alnx-x2+1.
(1)若曲线y=f(x)在x=1处的切线方程为4x-y+b=0,求实数a和b的值;
(2)若a<0,且对任意x1、x2∈(0,+∞),都|f(x1)-f(x2)|≥|x1-x2|,求a的取值范围.
【解析】第一问中利用f′(x)= -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
由已知得a-2=4,2-a=b,所以a=6,b=-4.
第二问中,利用当a<0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|f(x1)-f(x2)|=f(x1)-f(x2),|x1-x2|=x2-x1,
∴|f(x1)-f(x2)|≥|x1-x2|等价于f(x1)-f(x2)≥x2-x1,
即f(x1)+x1≥f(x2)+x2,结合构造函数和导数的知识来解得。
(1)f′(x)= -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
由已知得a-2=4,2-a=b,所以a=6,b=-4.
(2)当a<0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|f(x1)-f(x2)|=f(x1)-f(x2),|x1-x2|=x2-x1,
∴|f(x1)-f(x2)|≥|x1-x2|等价于f(x1)-f(x2)≥x2-x1,即f(x1)+x1≥f(x2)+x2,
令g(x)=f(x)+x=alnx-x2+x+1,g(x)在(0,+∞)上是减函数,
∵g′(x)= -2x+1=
-2x+1= (x>0),
(x>0),
∴-2x2+x+a≤0在x>0时恒成立,
∴1+8a≤0,a≤- ,又a<0,
,又a<0,
∴a的取值范围是

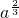 =
= ,则a=________,
,则a=________,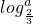 =________.
=________. 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案 -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0, -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0, -2x+1=
-2x+1= (x>0),
(x>0), ,又a<0,
,又a<0,
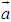 ,
,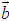 ,
,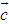 ,若
,若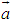 ∥
∥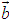 ,
,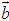 ∥
∥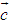 则
则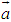 ∥
∥