
已知定点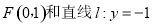 ,过点F且与直线
,过点F且与直线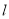 相切的动圆圆心为点M,记点M的轨迹为曲线E.
相切的动圆圆心为点M,记点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)若点A的坐标为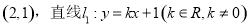 ,与曲线E相交于B,C两点,直线AB,AC分别交直线
,与曲线E相交于B,C两点,直线AB,AC分别交直线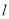 于点S,T.试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
于点S,T.试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
(1)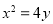 .(2)以线段
.(2)以线段 为直径的圆恒过两个定点
为直径的圆恒过两个定点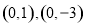 .
.
【解析】
试题分析:(1)根据抛物线的定义可知,点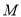 的轨迹是以点
的轨迹是以点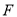 为焦点,
为焦点, 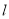 为准线的抛物线.
为准线的抛物线.
可得曲线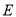 的方程为
的方程为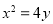 .
.
(2)设点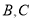 的坐标分别为
的坐标分别为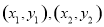 ,依题意得,
,依题意得,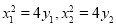 .
.
由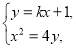 消去
消去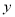 得
得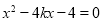 ,
,
应用韦达定理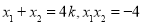 .
.
直线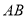 的斜率
的斜率 ,
,
故直线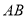 的方程为
的方程为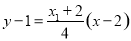 .
.
令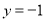 ,得
,得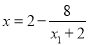 ,
,
得到点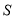 的坐标为
的坐标为 .点
.点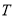 的坐标为
的坐标为 .
.
得到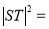
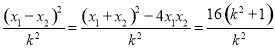 .
.
设线段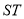 的中点坐标为
的中点坐标为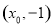 ,
,
而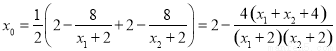
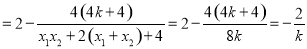 .
.
故以线段 为直径的圆的方程为
为直径的圆的方程为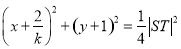
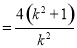 .
.
令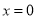 ,得
,得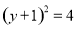 ,解得
,解得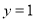 或
或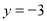 .
.
确定得到以线段 为直径的圆恒过两个定点
为直径的圆恒过两个定点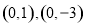 .
.
(1)由题意, 点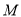 到点
到点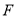 的距离等于它到直线
的距离等于它到直线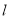 的距离,
的距离,
故点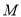 的轨迹是以点
的轨迹是以点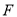 为焦点,
为焦点, 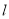 为准线的抛物线.
为准线的抛物线.
∴曲线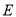 的方程为
的方程为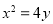 . 4分
. 4分
(2)设点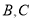 的坐标分别为
的坐标分别为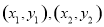 ,依题意得,
,依题意得,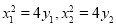 .
.
由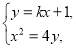 消去
消去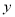 得
得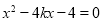 ,
,
∴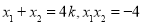 . 6分
. 6分
直线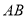 的斜率
的斜率 ,
,
故直线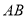 的方程为
的方程为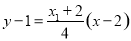 .
.
令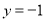 ,得
,得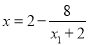 ,
,
∴点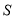 的坐标为
的坐标为 .
.
同理可得点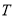 的坐标为
的坐标为 .
.
∴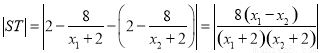
 .
.
∴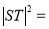
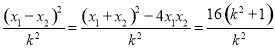 . 8分
. 8分
设线段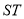 的中点坐标为
的中点坐标为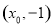 ,
,
则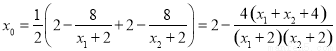
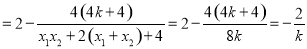 .
.
∴以线段 为直径的圆的方程为
为直径的圆的方程为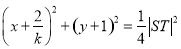
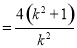 .
.
展开得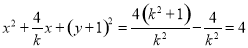 . 11分
. 11分
令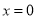 ,得
,得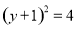 ,解得
,解得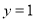 或
或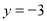 .
.
∴以线段 为直径的圆恒过两个定点
为直径的圆恒过两个定点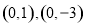 . 13分
. 13分
考点:抛物线的定义及其标准方程,直线方程,直线与圆锥曲线的位置关系,圆的方程.


科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试理科数学试卷(解析版) 题型:选择题
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的体积是
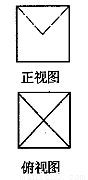
A.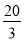 B.6 C.4 D.
B.6 C.4 D.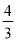
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试理科数学试卷(解析版) 题型:选择题
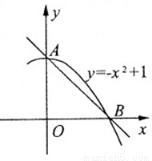
如图,设抛物线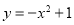 的顶点为A,与x 轴正半轴的交点为B,设抛物线与两坐标轴正半轴围成的区域为M,随机往M内投一点P, 则点P落在
的顶点为A,与x 轴正半轴的交点为B,设抛物线与两坐标轴正半轴围成的区域为M,随机往M内投一点P, 则点P落在 AOB内的概率是( )
AOB内的概率是( )
(A)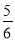 (B)
(B)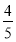
(C)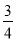 (D)
(D)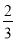
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试文科数学试卷(解析版) 题型:填空题
某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分……第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有 名.
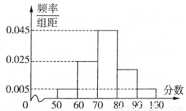
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试文科数学试卷(解析版) 题型:选择题
将函数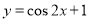 的图象向右平移
的图象向右平移 个单位,再向下平移1个单位后得到的函数图象对应的表达式为( )
个单位,再向下平移1个单位后得到的函数图象对应的表达式为( )
(A)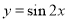 (B)
(B)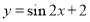
(C)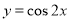 (D)
(D)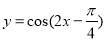
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三5月统一质量检测考试理科数学试卷(解析版) 题型:填空题
已知有限集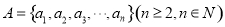 .如果A中元素
.如果A中元素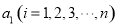 满足
满足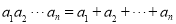 ,就称A为“复活集”,给出下列结论:
,就称A为“复活集”,给出下列结论:
①集合 是“复活集”;
是“复活集”;
②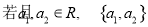 是“复活集”,则
是“复活集”,则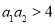 ;
;
③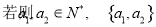 不可能是“复活集”;
不可能是“复活集”;
④若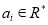 ,则“复活集”A有且只有一个,且
,则“复活集”A有且只有一个,且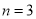 .
.
其中正确的结论是___________.(填上你认为所有正确的结论序号)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三5月统一质量检测考试理科数学试卷(解析版) 题型:选择题
三棱锥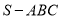 及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为( )
及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为( )
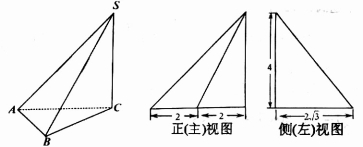
A. B.
B.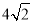 C.
C.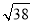 D.
D.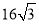
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三5月统一质量检测考试文科数学试卷(解析版) 题型:填空题
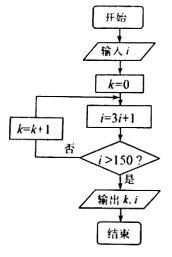
阅读如图所示的程序框图,若输入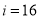 ,则输出的k值为____________.
,则输出的k值为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com