
【题目】已知椭圆的方程为![]() (
(![]() ),其离心率
),其离心率![]() ,
,![]() 分别为椭圆的左、右焦点,
分别为椭圆的左、右焦点,![]() 为椭圆上的点(
为椭圆上的点(![]() 不在
不在![]() 轴上),
轴上),![]() 周长为6.过椭圆右焦点
周长为6.过椭圆右焦点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() 面积为
面积为![]() .
.
(1)求椭圆的标准方程:
(2)求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)点![]() 为椭圆
为椭圆![]() 上一动点,连接
上一动点,连接![]() 、
、![]() ,设
,设![]() 的角平分线
的角平分线![]() 交椭圆
交椭圆![]() 的长轴于点
的长轴于点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( ).
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.

A. 互联网行业从业人员中90后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的20%
C. 互联网行业中从事运营岗位的人数90后比80前多
D. 互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: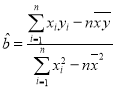 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)圆![]() 是以
是以![]() 为直径的圆,一直线
为直径的圆,一直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() 、
、![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面上定点![]() 到定直线
到定直线![]() 的距离
的距离![]() ,
,![]() 为该平面上的动点,过
为该平面上的动点,过![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且
,且![]() ;
;

(1)试建立适当的平面直角坐标系,求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() 、
、![]() 两点,交直线
两点,交直线![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是一个各位数字都不是0且没有重复数字的三位数,将组成
是一个各位数字都不是0且没有重复数字的三位数,将组成![]() 的3个数字按从小到大排成的三位数记为
的3个数字按从小到大排成的三位数记为![]() ,按从大到小排成的三位数记为
,按从大到小排成的三位数记为![]() ,(例如
,(例如![]() ,则
,则![]() ,
,![]() )阅读如图所示的程序框图,运行相应的程序,任意输入一个
)阅读如图所示的程序框图,运行相应的程序,任意输入一个![]() ,输出的结果
,输出的结果![]() =( )
=( )

A. 693 B. 594 C. 495 D. 792
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且2cos2![]() ·cosB-sin(A-B)sinB+cos(A+C)=-
·cosB-sin(A-B)sinB+cos(A+C)=-![]() .
.
(1)求cos A的值;
(2)若a=4![]() ,b=5,求
,b=5,求![]() 在
在![]() 方向上的投影.
方向上的投影.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com