
| MA |
| MB |
| MN |
| OF |
| NQ |
| OF |
| MA |
| MB |
| 5 |
| 5 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
|
| MA |
| MB |
| 1 |
| 2p |
| 1 |
| p |
| x1 |
| p |
| x2 |
| p |
| x12 |
| 2p |
| x1 |
| p |
| x2 |
| p |
| x22 |
| 2p |
|
| x1+x2 |
| 2 |
| x1x2 |
| 2p |
| MN |
| OF |
| NQ |
| OF |
| MA |
| MB |
| MA |
| MB |
| NF |
| AB |
| x1+x2 ) |
| 2p |
| NF |
| AB |
| NF |
| AB |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
|
| x12x22 |
| 4p2 |
| p2 |
| 4 |
| MA |
| MB |
| 1 |
| 2p |
| 1 |
| p |
| x1 |
| p |
| x2 |
| p |
| x12 |
| 2p |
| x1 |
| p |
| x1 |
| p |
| x12 |
| 2p |
| x2 |
| p |
| x22 |
| 2p |
|
|
| x1+x2 |
| 2 |
| x1x2 |
| 2p |
| NQ |
| OF |
| p |
| 2 |
| p |
| 2 |
| MN |
| OF |
| p |
| 2 |
| MN |
| OF |
| MA |
| MB |
| MA |
| MB |
| NF |
| AB |
| x1+x2 ) |
| 2p |
| NF |
| AB |
| NF |
| AB |
| NF |
| p2k2+p2 |
| 5 |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |


 √ыћвљрЊнѕµЅ–ір∞Є
√ыћвљрЊнѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
![]() ÷±ѕяABєэ≈„ќпѕяx2=2py£®p>0£©µƒљєµгF£ђ≤Ґ”л∆дѕаљї”ЏA°ҐBЅљµг£ђQ «ѕяґќABµƒ÷–µг£ђM «≈„ќпѕяµƒ„Љѕя”лy÷бµƒљїµг£ђO «„ш±к‘≠µг.
÷±ѕяABєэ≈„ќпѕяx2=2py£®p>0£©µƒљєµгF£ђ≤Ґ”л∆дѕаљї”ЏA°ҐBЅљµг£ђQ «ѕяґќABµƒ÷–µг£ђM «≈„ќпѕяµƒ„Љѕя”лy÷бµƒљїµг£ђO «„ш±к‘≠µг.
£®Ґс£©«у![]() µƒ»°÷µЈґќІ£ї
µƒ»°÷µЈґќІ£ї
£®Ґт£©єэA°ҐBЅљµгЈ÷±р„чіЋ≈„ќпѕяµƒ«–ѕя£ђЅљ«–ѕяѕаљї”ЏNµг.
«у÷§£Ї![]() £ї
£ї
£®Ґу£©»фp «≤їќ™1µƒ’э’ы э£ђµ±![]() £ђ°чABNµƒ√жїэµƒ»°÷µЈґќІќ™£џ5
£ђ°чABNµƒ√жїэµƒ»°÷µЈґќІќ™£џ5![]() £ђ20
£ђ20![]() £Ё ±£ђ«уЄ√≈„ќпѕяµƒЈљ≥ћ.
£Ё ±£ђ«уЄ√≈„ќпѕяµƒЈљ≥ћ.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
![]() ÷±ѕяABєэ≈„ќпѕяx2=2py£®p>0£©µƒљєµгF£ђ≤Ґ”л∆дѕаљї”ЏA°ҐBЅљµг£ђQ «ѕяґќABµƒ÷–µг£ђM «≈„ќпѕяµƒ„Љѕя”лy÷бµƒљїµг£ђO «„ш±к‘≠µг.
÷±ѕяABєэ≈„ќпѕяx2=2py£®p>0£©µƒљєµгF£ђ≤Ґ”л∆дѕаљї”ЏA°ҐBЅљµг£ђQ «ѕяґќABµƒ÷–µг£ђM «≈„ќпѕяµƒ„Љѕя”лy÷бµƒљїµг£ђO «„ш±к‘≠µг.
£®Ґс£©«у![]() µƒ»°÷µЈґќІ£ї
µƒ»°÷µЈґќІ£ї
£®Ґт£©єэA°ҐBЅљµгЈ÷±р„чіЋ≈„ќпѕяµƒ«–ѕя£ђЅљ«–ѕяѕаљї”ЏNµг.
«у÷§£Ї![]() £ї
£ї
£®Ґу£©»фp «≤їќ™1µƒ’э’ы э£ђµ±![]() £ђ°чABNµƒ√жїэµƒ»°÷µЈґќІќ™£џ5
£ђ°чABNµƒ√жїэµƒ»°÷µЈґќІќ™£џ5![]() £ђ20
£ђ20![]() £Ё ±£ђ«уЄ√≈„ќпѕяµƒЈљ≥ћ.
£Ё ±£ђ«уЄ√≈„ќпѕяµƒЈљ≥ћ.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
(1)«у÷§![]() µƒ»°÷µЈґќІ£ї
µƒ»°÷µЈґќІ£ї
(2)єэA°ҐBЅљµгЈ÷±р„чіЋ≈„ќпѕяµƒ«–ѕя£ђЅљ«–ѕяѕаљї”ЏNµг£ђ
«у÷§£Ї![]() £ї
£ї
(3)…и÷±ѕяAB”лx÷б°Ґy÷бµƒЅљЄцљїµгЈ÷±рќ™KЇЌL£ђµ±![]() =4p2£ђ°чABNµƒ√жїэµƒ»°÷µЈґќІѕёґ®ќ™[
=4p2£ђ°чABNµƒ√жїэµƒ»°÷µЈґќІѕёґ®ќ™[![]() ] ±£ђ«уґѓѕяґќKLµƒємЉ£Ћщ–ќ≥…µƒ∆љ√ж«ш”тµƒ√жїэ.
] ±£ђ«уґѓѕяґќKLµƒємЉ£Ћщ–ќ≥…µƒ∆љ√ж«ш”тµƒ√жїэ.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї2011ƒкєгґЂ °ЄяњЉ э—ІµЏ»э¬÷Єіѕ∞ЊЂ±аƒ£ƒв ‘Њн08£®јнњ∆£©£®љвќц∞ж£© ћв–Ќ£Їљвірћв
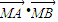 µƒ»°÷µЈґќІ£ї
µƒ»°÷µЈґќІ£ї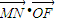 =0£ђ
=0£ђ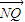 °ќ
°ќ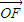 £ї
£ї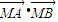 =4P2£ђ°чABNµƒ√жїэµƒ»°÷µЈґќІќ™[5
=4P2£ђ°чABNµƒ√жїэµƒ»°÷µЈґќІќ™[5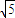 £ђ20
£ђ20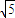 ] ±£ђ«уЄ√≈„ќпѕяµƒЈљ≥ћ£Ѓ
] ±£ђ«уЄ√≈„ќпѕяµƒЈљ≥ћ£Ѓ≤йњіір∞ЄЇЌљвќц>>
∞ўґ»÷¬–≈ - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com