
【题目】![]() 设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab > cd,则
设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab > cd,则 ![]() +
+![]() >
>![]() +
+ ![]() ;(2)
;(2) ![]() +
+![]() >
> ![]() +
+ ![]() 是|a-b| < |c-d|的充要条件
是|a-b| < |c-d|的充要条件
(1)(I)若ab![]() cd,则
cd,则![]() +
+![]()
![]()
![]() +
+![]()
(2)(II)![]() +
+![]()
![]()
![]() +
+![]() 是|a-b|
是|a-b|![]() |c-d|的充要条件
|c-d|的充要条件
【答案】
(1)
见解答
(2)
见解答
【解析】(1)因为![]() +
+![]() )2=a+b+2
)2=a+b+2![]() ,(
,(![]() +
+![]() )2=c+d+2
)2=c+d+2![]()
由题设a+b=c+d,ab![]() cd,得(
cd,得(![]() +
+![]() )2
)2![]() (
(![]() +
+![]() )2
)2
因此![]() +
+![]()
![]()
![]() +
+![]() 。
。
(II)(i)若|a-b|![]() |c-d|,则(a-b)2
|c-d|,则(a-b)2![]() (c-d)2,即(a+b)2-4ab
(c-d)2,即(a+b)2-4ab![]() (c+d)2-4cd,
(c+d)2-4cd,
因为a+b=c+d,所以ab![]() cd
cd
由(I)得![]() +
+![]()
![]()
![]() +
+![]()
(ii)若![]() +
+![]()
![]()
![]() +
+![]() , 则(
, 则(![]() +
+![]() )2
)2![]() (
(![]() +
+![]() )2,即a+b+2
)2,即a+b+2![]()
![]() c+d+2
c+d+2![]() ,因为a+b=c+d,
,因为a+b=c+d,
所以ab![]() cd
cd
于是(a-b)2=(a+b)2-4ab![]() (c+d)2-4cd=(c-d)2
(c+d)2-4cd=(c-d)2
因此|a-b|![]() |c-d|,综上所述,
|c-d|,综上所述,![]() +
+![]()
![]()
![]() +
+![]() 是|a-b|
是|a-b|![]() |c-d|的充要条件
|c-d|的充要条件
【考点精析】关于本题考查的不等式的证明,需要了解不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(已知函数f(x)=|2x+1|+|x﹣2|,不等式f(x)≤2的解集为M.
(1)求M;
(2)记集合M的最大元素为m,若正数a,b,c满足abc=m, 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D=  ,给出下列四个命题:
,给出下列四个命题:
P1:(x,y)∈D,x+y+1≥0;
P2:(x,y)∈D,2x﹣y+2≤0;
P3:(x,y)∈D, ![]() ≤﹣4;
≤﹣4;
P4:(x,y)∈D,x2+y2≤2.
其中真命题的是( )
A.P1 , P2
B.P2 , P3
C.P2 , P4
D.P3 , P4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+ax﹣ ![]() (a∈R)在x=2处的切线经过点(﹣4,2ln2)
(a∈R)在x=2处的切线经过点(﹣4,2ln2)
(1)讨论函数f(x)的单调性
(2)若不等式 ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 已知椭圆C:
已知椭圆C:![]() +
+![]() =1,(a
=1,(a![]() b
b![]() 0)的离心率为
0)的离心率为![]() ,点(2,
,点(2,![]() )在C上
)在C上
(1)求C的方程;
(2)直线l不经过原点O,且不平行于坐标轴,l与C有两个交点A,B,线段AB中点为M,证明:直线OM的斜率与直线l的斜率乘积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面![]() 与此长方体的面相交,交线围成一个正方形。
与此长方体的面相交,交线围成一个正方形。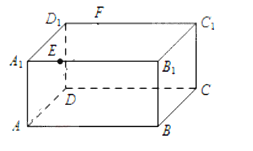
(1)(I)在图中画出这个正方形(不必说明画法与理由);
(2)(II)求平面 把该长方体分成的两部分体积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(2015·新课标Ⅱ)设函数f‘(x)是奇函数f(x)(x![]() R)的导函数,f(-1)=0,当x
R)的导函数,f(-1)=0,当x![]() 0时,xf'(x)-f(x)
0时,xf'(x)-f(x)![]() 0,则使得f(x)
0,则使得f(x)![]() 0成立的x的取值范围是()
0成立的x的取值范围是()
A.(-![]() ,-1)
,-1)![]() (0,1)
(0,1)
B.(-1,0)![]() (1,+
(1,+![]() )
)
C.(-![]() ,-1)
,-1)![]() (-1,0)
(-1,0)
D.(0,1)![]() (1,+
(1,+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)已知函数f(x)=x3+ax+![]() , g(x)=-lnx.
, g(x)=-lnx.
(1)当a为何值时,x轴为曲线y=f(x)的切线;
(2)用min{m,n} 表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(x>0),,讨论h(x)零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)在直角坐标系xOy中,直线l的参数方程为 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,![]() c的极坐标方程为
c的极坐标方程为![]() =2
=2![]() sin
sin![]() .
.
(1)写出![]() c的直角坐标方程;
c的直角坐标方程;
(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com