
如图,已知三棱锥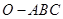 的侧棱
的侧棱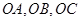 两两垂直,且
两两垂直,且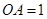 ,
,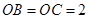 ,
, 是
是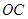 的中点.(1)求
的中点.(1)求 点到面
点到面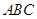 的距离;(2)求二面角
的距离;(2)求二面角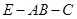 的正弦值.
的正弦值.
(1)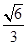 ;(2)
;(2)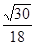 .
.
解析试题分析:(1)先建系写出各点坐标,求面ABC的法向量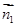 ,然后求
,然后求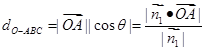 ;(2)先求面EAB的法向量
;(2)先求面EAB的法向量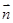 ,再求
,再求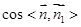 ,然后结合图形判断二面角E-AB-C的范围,得其余弦值的正负.
,然后结合图形判断二面角E-AB-C的范围,得其余弦值的正负.
试题解析:(1)取 的中点
的中点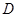 ,连
,连 、
、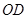
∵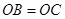 ,则
,则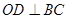 、
、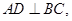 ∴
∴ 面
面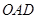 .过点O作
.过点O作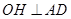 于H,
于H,
则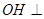 面
面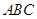 ,
,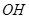 的长就是所要求的距离.
的长就是所要求的距离.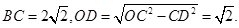 3分
3分
∵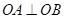 、
、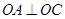 ,∴
,∴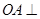 平面
平面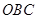 ,则
,则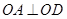 .
.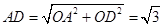 ,在直角三角形
,在直角三角形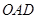 中,有
中,有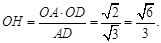 6分
6分
(另解:由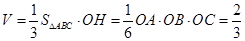 知,
知,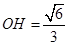 )
)
(2)连结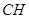 并延长交
并延长交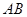 于
于 ,连结
,连结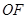 、
、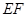 .
.
∵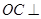 面OAB,∴
面OAB,∴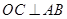 .又∵
.又∵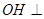 面ABC,∴
面ABC,∴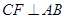 ,
,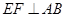 ,
,
则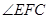 就是所求二面角的平面角. 9分
就是所求二面角的平面角. 9分
作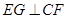 于
于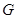 ,则
,则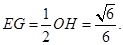
在直角三角形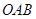 中,
中,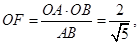
在直角三角形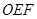 中,
中, 12分
12分 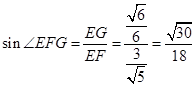 ,故所求的正弦值是
,故所求的正弦值是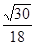 14分
14分
方法二: (1)以 为原点,
为原点,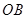 、
、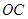 、
、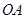 分别为
分别为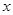 、
、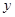 、
、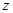 轴建立空间直角坐标系.
轴建立空间直角坐标系.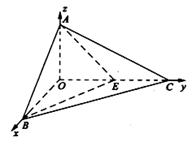
则有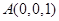 、
、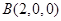 、
、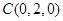 、
、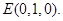 2分
2分
设平面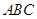 的法向量为
的法向量为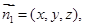
则由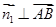 知:
知: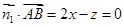 ;
;
由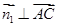 知:
知: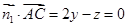 .取
.取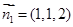 , 4分
, 4分
则点


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
如图,已知多面体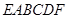 的底面
的底面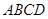 是边长为
是边长为 的正方形,
的正方形,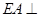 底面
底面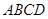 ,
, ,且
,且 .
.
(Ⅰ )求多面体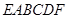 的体积;
的体积;
(Ⅱ )求证:平面EAB⊥平面EBC;
(Ⅲ)记线段CB的中点为K,在平面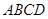 内过K点作一条直线与平面
内过K点作一条直线与平面 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图1,在四棱锥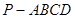 中,
中, 底面
底面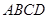 ,面
,面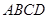 为正方形,
为正方形,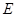 为侧棱
为侧棱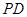 上一点,
上一点, 为
为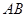 上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.
上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.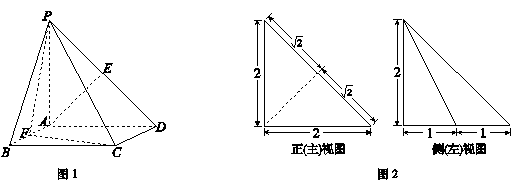
(Ⅰ)求四面体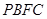 的体积;
的体积;
(Ⅱ)证明: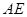 ∥平面
∥平面 ;
;
(Ⅲ)证明:平面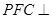 平面
平面 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱柱


(I)当正视方向与向量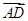 的方向相同时,画出四棱锥
的方向相同时,画出四棱锥 的正视图(要求标出尺寸,并写出演算过程);
的正视图(要求标出尺寸,并写出演算过程);
(II)若M为PA的中点,求证:求二面角
(III)求三棱锥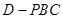 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com