
【题目】南京江北新区是第十三个国家级新区,随着新区的经济发展,老城区将不断的进行开发和改造,如图为边长为4km的正三角形![]() 区域,
区域,![]() 分别在三边
分别在三边![]() 上,且
上,且![]() 为
为![]() 的中点,
的中点,![]() ,现将对正三角形
,现将对正三角形![]() 区域进行规划,规划
区域进行规划,规划![]() 区域为娱乐广场,其他区域为生活居住区.
区域为娱乐广场,其他区域为生活居住区.

(1)若![]() ,求娱乐广场
,求娱乐广场![]() 的面积;
的面积;
(2)求生活区域的面积![]() 的最大值,并写出
的最大值,并写出![]() 取得最大值时
取得最大值时![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 5 |
| 0 |
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数![]() 的解析式;
的解析式;
(2)将![]() 图象上所有点向左平行移动
图象上所有点向左平行移动![]() 个单位长度,并把图象上所有点的横坐标缩短为原来的
个单位长度,并把图象上所有点的横坐标缩短为原来的![]() (纵坐标不变),得到
(纵坐标不变),得到![]() 的图象.若
的图象.若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值;
的最小值;
(3)在(2)条件下,求![]() 在
在![]() 上的增区间.
上的增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在世界数学史上是一个伟大的创造,算筹实际上是一根根同样长短的小木棍,如图,算筹表示数1~9的方法的一种.

例如:163可表示为“![]() ”27可表示为“
”27可表示为“![]() ”问现有8根算筹可以表示三位数的个数(算筹不能剩余)为( )
”问现有8根算筹可以表示三位数的个数(算筹不能剩余)为( )
A. 48 B. 60 C. 96 D. 120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个人打靶,打了10发子弹,有7发子弹中靶,因此这个人中靶的概率为![]()
B.某地发行福利彩票,其回报率为![]() ,有个人花了100元钱买彩票,一定会有47元回报
,有个人花了100元钱买彩票,一定会有47元回报
C.根据最小二乘法求得的回归直线![]() 一定经过样本中心点
一定经过样本中心点![]()
D.大量试验后,可以用频率近似估计概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)设数列![]() 的前
的前![]() 项和为
项和为![]() .已知
.已知![]() ,
, ![]() ,
, ![]() .
.
(1)写出![]() 的值,并求数列
的值,并求数列![]() 的通项公式;
的通项公式;
(2)记![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() ;
;
(3)若数列![]() 满足
满足![]() ,
, ![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定集合![]() (
(![]() 且
且![]() ),定义点集
),定义点集![]() ,若对任意点
,若对任意点![]() ,存在
,存在![]() ,使得
,使得![]() (
(![]() 为坐标原点).则称集合
为坐标原点).则称集合![]() 具有性质
具有性质![]() ,给出一下四个结论:
,给出一下四个结论:
①![]() 其有性质
其有性质![]() ;
;
②![]() 具有性质
具有性质![]() ;
;
③若集合![]() 具有性质
具有性质![]() ,则
,则![]() 中一定存在两数
中一定存在两数![]() ,使得
,使得![]() ;
;
④若集合![]() 具有性质
具有性质![]() .
.![]() 是
是![]() 中任一数,则在
中任一数,则在![]() 中一定存在
中一定存在![]() ,使得
,使得![]() .
.
其中正确结论有___________(填上你认为所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
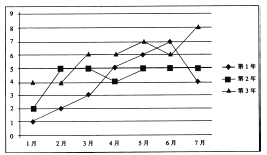
(1)试问这3年的前7个月中哪个月的平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份 | 1 | 2 | 3 | 4 |
利润 | 4 | 4 | 6 | 6 |
相关公式:  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月某城市国际马拉松赛正式举行,组委会对
月某城市国际马拉松赛正式举行,组委会对![]() 名裁判人员进行业务培训,现按年龄(单位:岁)进行分组统计:第
名裁判人员进行业务培训,现按年龄(单位:岁)进行分组统计:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如下:
,得到的频率分布直方图如下:
(1)培训前组委会用分层抽样调查方式在第![]() 组共抽取了
组共抽取了![]() 名裁判人员进行座谈,若将其中抽取的第
名裁判人员进行座谈,若将其中抽取的第![]() 组的人员记作
组的人员记作![]() ,第
,第![]() 组的人员记作
组的人员记作![]() ,第
,第![]() 组的人员记作
组的人员记作![]() ,若组委会决定从上述
,若组委会决定从上述![]() 名裁判人员中再随机选
名裁判人员中再随机选![]() 人参加新闻发布会,要求这
人参加新闻发布会,要求这![]() 组各选
组各选![]() 人,试求裁判人员
人,试求裁判人员![]() 不同时被选择的概率;
不同时被选择的概率;
(2)培训最后环节,组委会决定从这![]() 名裁判中年龄在
名裁判中年龄在![]() 的裁判人员里面随机选取
的裁判人员里面随机选取![]() 名参加业务考试,设年龄在
名参加业务考试,设年龄在![]() 中选取的人数为
中选取的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某林业部门为了保证植树造林的树苗质量,对甲、乙两家供应的树苗进行根部直径检测,现从两家供应的树苗中各随机抽取10株树苗检测,测得根部直径如下(单位:mm):
甲 | 27 | 11 | 21 | 10 | 19 | 09 | 22 | 13 | 15 | 23 |
乙 | 15 | 20 | 27 | 17 | 21 | 14 | 16 | 18 | 24 | 18 |
(1)画出甲、乙两家抽取的10株树苗根部直径的茎叶图,并根据茎叶图对甲、乙两家树苗进行比较,写出两个统计结论;
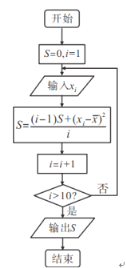
(2)设抽测的10株乙家树苗根部直径的平均值为![]() ,将这10株树苗直径依次输入程序框图中,求输出的S的值,并说明其统计学的意义.
,将这10株树苗直径依次输入程序框图中,求输出的S的值,并说明其统计学的意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com