
| 5-x | 5x+2 |
| 5-x |
| 5x+2 |
| x-5 |
| 5x+2 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |


科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称点(x0,x0)为函数f(x)的不动点.
(Ⅰ)已知函数f(x)=ax2+bx-b(a≠0)有不动点(1,1)和(-3,-3),求a、b的值;
(Ⅱ)若对于任意实数b,函数f(x)=ax2+bx-b总有两个相异的不动点,求实数a的取值范围;
(Ⅲ)(理)若定义在实数集R上的奇函数g(x)存在(有限的)n个不动点,求证:n必为奇数.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省武汉市武昌区高二(上)10月月考数学试卷(解析版) 题型:填空题
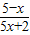 ≥0的解集是 .
≥0的解集是 .查看答案和解析>>
科目:高中数学 来源: 题型:
(09年崇文区二模理)已知![]() 是定义在R上的不恒为零的函数,且对于任意实数
是定义在R上的不恒为零的函数,且对于任意实数
![]() 满足:
满足:
![]() ,
,![]()
考察下列结论:
①![]()
②数列{an}为等比例数列;
③数列{bn}为等差数列。
其中正确的结论是 ( )
A.①②③ B.①③ C.①② D.②③查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com