
����Ŀ����ijУ��һ�꼶ѧ���μ����������������ͳ�ƣ������ȡM��ѧ����Ϊ�������õ���M��ѧ���μ���������Ĵ��������ݴ�����������Ƶ����Ƶ�ʵ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ���£�
���� | Ƶ�� | Ƶ�� |
[10��15�� | 10 | 0.25 |
[15��20�� | 25 | n |
[20��25�� | m | p |
[25��30�� | 2 | 0.05 |
�ϼ� | M | 1 |

��1���������M��p��ͼ��a��ֵ��
��2������У��һѧ����360�ˣ��Թ��Ƹ�У��һѧ���μ���������Ĵ���������[15��20���ڵ�������
��3������ȡ�����У��Ӳμ���������Ĵ���������20�ε�ѧ������ѡ2�ˣ����оٳ����л����¼�����������1�˲μ������������������[20��25���ڵĸ��ʣ�
���𰸡���1��0.125����2��5����3��![]()
��������
��1����Ƶ��=![]() �����������M��p��ͼ��a��ֵ����2����Ƶ����Ƶ�ʵ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ������μ����������ƽ����������3���������У�����[20��25���ڵ�����Ϊ3���ɷֱ��ΪA��B��C������[25��30]�ڵ�����Ϊ2���ɷֱ��Ϊa��b���ɴ������оٷ����������1�˲μ������������������[20��25���ڵĸ��ʣ�
�����������M��p��ͼ��a��ֵ����2����Ƶ����Ƶ�ʵ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ������μ����������ƽ����������3���������У�����[20��25���ڵ�����Ϊ3���ɷֱ��ΪA��B��C������[25��30]�ڵ�����Ϊ2���ɷֱ��Ϊa��b���ɴ������оٷ����������1�˲μ������������������[20��25���ڵĸ��ʣ�
��1���ɷ���[10��15���ڵ�Ƶ����10��Ƶ����0.25֪��![]() ������M=40��
������M=40��
��ΪƵ��֮��Ϊ40������![]() ��
��
��Ϊa�Ƕ�Ӧ����[15��20����Ƶ���������̣�����![]() ��
��
��2����Ϊ��У����ѧ����360�ˣ�����[15��20���ڵ�Ƶ����0.625��
���Թ��Ƹ�У����ѧ���μ���������Ĵ����ڴ������ڵ�����Ϊ360��0.625=225�ˣ�
��3����������μ���������Ĵ���������20�ε�ѧ������3+2=5��
��������[20��25���ڵ���Ϊ{a1��a2��a3}��������[25��30���ڵ���Ϊ{b1��b2}��
����ѡ2�˹��У�a1��a2������a1��a3������a1��b1������a1��b2������a2��a3������a2��b1������a2��b2������a3��b1������a3��b2������b1��b2��10���������9�֣�
�����˶���[20��25���ڹ��У�a1��a2������a1��a3������a2��a3��3�������
����һ�˲μ������������������[20��25���ڵĸ���Ϊ![]() ��
��


 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������Ϊ2������Ϊ
������Ϊ2������Ϊ![]() �ĵȱ����У���ǰ
�ĵȱ����У���ǰ![]() ���Ϊ
���Ϊ![]() .
.
��1����![]() ��ʾ
��ʾ![]() ��
��
��2���Ƿ������Ȼ��![]() ��
��![]() ��ʹ��
��ʹ��![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ ![]() ��a��b��0������P��2��1������������Ϊ
��a��b��0������P��2��1������������Ϊ ![]() ��
��
��������Բ�ķ��̣�
������OΪ����ԭ�㣬����Բ������������M��N���� ![]() ��ֱ��PM��PN�ֱ���Բ��A��B��
��ֱ��PM��PN�ֱ���Բ��A��B��
��i����֤��ֱ��AB�����㣬�������������ꣻ
��ii�����OAB��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() ��Բ
��Բ![]() ��ֱ��
��ֱ��![]() �ཻ��
�ཻ��![]() ���㣬��
���㣬��![]() ��
��![]() Ϊ����ԭ�㣩����ʵ��
Ϊ����ԭ�㣩����ʵ��![]() ��ֵΪ�� ��
��ֵΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ΪԲ
ΪԲ![]() ��һ�㣬��Բ
��һ�㣬��Բ![]() �ϴ���һ��
�ϴ���һ��![]() ��ʹ��
��ʹ��![]() ��������
��������![]() ��ȡֵ��Χ��____________��
��ȡֵ��Χ��____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC����ԭ��O��0��0������ֱ��y=2x��8�����ڵ�P��4��0����
��1����ԲC�ķ��̣�
��2����ֱ֪��l�����㣨4, 5��������ԲC�ཻ��M��N���㣬��|MN|=2�����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC���ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c��2acosC=bcosC+ccosB��
��1�����C�Ĵ�С��
��2����c=![]() ��a2+b2=10������ABC�������
��a2+b2=10������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����л��������5�����飬�����������ʾ��
������ | ��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
x | 555 | 559 | 551 | 563 | 552 |
y | 601 | 605 | 597 | 599 | 598 |
����5��������y����������������س�ȡ�������ݣ���������һ������600�ĸ��ʣ�
������������y����x�����Իع鷽�� ![]() ����Ԥ�������xΪ570ʱ������y��ֵ��
����Ԥ�������xΪ570ʱ������y��ֵ��
�������ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ ![]() =
=  ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��ԲC��![]() ��������Ϊ
��������Ϊ![]() ���ҹ���
���ҹ���![]() ������Բ����A��ֱ��
������Բ����A��ֱ��![]() ������MΪֱ��
������MΪֱ��![]() �ϵĶ�������BΪ��Բ�Ҷ��㣬ֱ��BM����ԲC��P
�ϵĶ�������BΪ��Բ�Ҷ��㣬ֱ��BM����ԲC��P
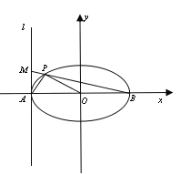
��1������ԲC�ķ��̣�
��2����֤��![]() ��
��
��3������![]() �Ƿ�Ϊ��ֵ�����Ƕ�ֵ��������ö�ֵ�������Ƕ�ֵ����˵�����ɣ�
�Ƿ�Ϊ��ֵ�����Ƕ�ֵ��������ö�ֵ�������Ƕ�ֵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com