
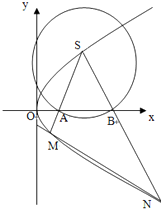
 已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.
已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.分析 (1)设S(x0,y0)(y0>0),由已知得F($\frac{1}{4}$,0),则|SF|=x0+$\frac{1}{4}$=$\frac{5}{4}$,由此能求出点S的坐标.
(2)设直线SA的方程为y-1=k(x-1)(k≠0),M(x1,y1),与抛物线方程联立得ky2-y+1-k=0,求出M,N的坐标导出直线MN的斜率为定值,设出直线MN的方程与抛物线方程联立,求出△SMN面积,换元,利用导数的方法求△SMN面积的最大值.
解答 解:(1)设S(x0,y0)(y0>0),由已知得F($\frac{1}{4}$,0),则|SF|=x0+$\frac{1}{4}$=$\frac{5}{4}$,
∴x0=1,
∴y0=1,∴点S的坐标是(1,1)------------------------(2分)
(2)设直线SA的方程为y-1=k(x-1)(k≠0),M(x1,y1),
与抛物线方程联立得ky2-y+1-k=0,
∴y1=$\frac{1}{k}$-1,∴M($\frac{(1-k)^{2}}{{k}^{2}}$,$\frac{1}{k}$-1).
由已知SA=SB,∴直线SB的斜率为-k,
∴N($\frac{(1+k)^{2}}{{k}^{2}}$,-$\frac{1}{k}$-1),∴kMN=-$\frac{1}{2}$
设直线MN的方程为y=-$\frac{1}{2}$x+b,即x+2y-2b=0,b∈(-$\frac{1}{2}$,$\frac{3}{2}}$),
与抛物线方程联立,消去x,可得y2+2y-2b=0,
∴|MN|=$\sqrt{1+4}$•$\sqrt{4+8b}$=2$\sqrt{5}$•$\sqrt{1+2b}$,
S到直线MN的距离d=$\frac{|3-2b|}{\sqrt{5}}$,
∴S△SMN=$\frac{1}{2}•2\sqrt{5}•\sqrt{1+2b}•\frac{|3-2b|}{\sqrt{5}}$=$\sqrt{1+2b}$(3-2b),
令t=$\sqrt{1+2b}$,t∈(0,2),S△SMN=t(4-t2),
S△SMN′=-3t2+4=0,t=$\frac{2\sqrt{3}}{3}$,
∴t=$\frac{2\sqrt{3}}{3}$,△SMN面积的最大值为$\frac{16\sqrt{3}}{9}$.
点评 本题主要考查直线与圆锥曲线的综合应用能力,涉及到直线与圆锥曲线的相关知识,导数知识的运用,知识综合性强.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:选择题
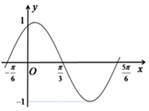 如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{6}$,$\frac{5π}{6}$]上的图象.为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上所有的点( )
如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{6}$,$\frac{5π}{6}$]上的图象.为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上所有的点( )| A. | 向左平移$\frac{π}{3}$个单位,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$倍 | |
| B. | 向左平移$\frac{π}{3}$个单位,再把所得各点的横坐标伸长到原来的2倍 | |
| C. | 向左平移$\frac{π}{6}$个单位,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$倍 | |
| D. | 向左平移$\frac{π}{6}$个单位,再把所得各点的横坐标伸长到原来的2倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
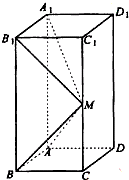 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com