
【题目】如图,在六面体ABCD﹣A1B1C1D1中,AA1//CC1,A1B=A1D,AB=AD.求证:
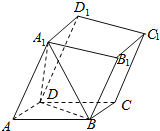
(1)AA1⊥BD;
(2)BB1//DD1.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
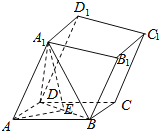
(1)取BD中点E,连接AE、A1E,证明BD⊥平面A1AE,即可证得结论;
(2)证明BB1//CC1DD1//CC1,再利用平行公理,即可证得结论.
(1)取BD中点E,连接AE、A1E
∵△ABD中,AB=AD,E为BD中点
∴AE⊥BD,同理可得A1E⊥BD,
∵AE、A1E平面A1AE,AE![]() A1E=E
A1E=E
∴BD⊥平面A1AE,
∵AA1平面A1AE,∴AA1⊥BD;
(2)∵AA1//CC1,AA1平面AA1B1B,CC1平面AA1B1B,
∴CC1//平面AA1B1B
∵CC1平面CC1B1B,平面CC1B1B![]() 平面AA1B1B=BB1
平面AA1B1B=BB1
∴BB1//CC1,同理可得DD1//CC1,
∴BB1//DD1.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,点
上的动点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求直线![]() 及曲线
及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与直线
与直线![]() 交于点
交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() (与原点不重合),求
(与原点不重合),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷(Dirichlet,1805~1859)在数学领域成就显著.19世纪,狄利克雷定义了一个“奇怪的函数” 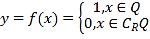 其中R为实数集,Q为有理数集.则关于函数
其中R为实数集,Q为有理数集.则关于函数![]() 有如下四个命题,正确的为( )
有如下四个命题,正确的为( )
A.函数![]() 是偶函数
是偶函数
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一个不为零的有理数T,![]() 对任意的
对任意的![]() 恒成立
恒成立
D.不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆C:![]() (
(![]() ),称圆心在原点O,半径为
),称圆心在原点O,半径为![]() 的圆是椭圆C的“卫星圆”.若椭圆C的离心率
的圆是椭圆C的“卫星圆”.若椭圆C的离心率![]() ,点
,点![]() 在C上.
在C上.
(1)求椭圆C的方程和其“卫星圆”方程;
(2)点P是椭圆C的“卫星圆”上的一个动点,过点P作直线![]() ,
,![]() 使得
使得![]()
![]()
![]() ,与椭圆C都只有一个交点,且
,与椭圆C都只有一个交点,且![]() ,
,![]() 分别交其“卫星圆”于点M,N,证明:弦长
分别交其“卫星圆”于点M,N,证明:弦长![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“回文数”是指从左到右与从右到左读都一样的正整数,如22,121,3553等.显然2位“回文数”共9个:11,22,33,…,99.现从9个不同2位“回文数”中任取1个乘以4,其结果记为X;从9个不同2位“回文数”中任取2个相加,其结果记为Y.
(1)求X为“回文数”的概率;
(2)设随机变量![]() 表示X,Y两数中“回文数”的个数,求
表示X,Y两数中“回文数”的个数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查.现在按课外阅读时间的情况将学生分成三类:![]() 类(不参加课外阅读),
类(不参加课外阅读),![]() 类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),
类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),![]() 类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
|
|
| |
男生 |
| 5 | 3 |
女生 |
| 3 | 3 |
(1)求出表中![]() ,
,![]() 的值;
的值;
(2)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | ||
不参加课外阅读 | ||||
参加课外阅读 | ||||
总计 |
P(K≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com