
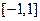 上的函数
上的函数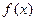 满足
满足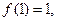 且当
且当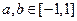 时,
时,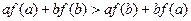 ;
;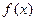 在
在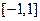 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.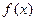 是奇函数, 不等式
是奇函数, 不等式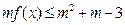 对所有的
对所有的 恒成立,
恒成立,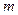 的取值范围.
的取值范围.科目:高中数学 来源:不详 题型:解答题
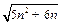 ,汛期共计约40天,当前水库水位为220(标高),而水库警戒水位是400(标高),水库共有水闸15个,每开启一个泄洪,一天可使水位下降4(标高).
,汛期共计约40天,当前水库水位为220(标高),而水库警戒水位是400(标高),水库共有水闸15个,每开启一个泄洪,一天可使水位下降4(标高).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
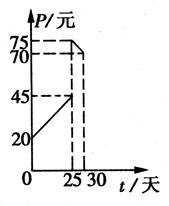
| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 |  10 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com