
|
| 12 |
| k |
| 24 |
| k |
| 144 |
| k2 |
| 96 |
| k |
| ||
| 3 |
| ||
| 3 |
| 10 |
| 10 |
11-2
| ||
| 3 |
11+2
| ||
| 3 |
| y1-y2 |
| x1-x2 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
 某学校招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高(单位:cm)编成如下茎叶图:若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“拿高个子”,如果用分层抽样的方法从“高小子”和“攀高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是
某学校招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高(单位:cm)编成如下茎叶图:若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“拿高个子”,如果用分层抽样的方法从“高小子”和“攀高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 3 |
A、f(x)的图象可以由g(x)的图象向左平移
| ||
B、f(x)的图象可以由g(x)的图象向右平移
| ||
C、f(x)的图象可以由g(x)的图象关于直线x=
| ||
D、f(x)的图象可以由g(x)的图象关于直线x=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
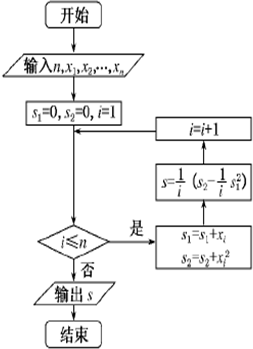 1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )
1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、2lgx+lgy=2lgx+2lgy |
| B、2lg(x+y)=2lgx•2lgy |
| C、2lgx•lgy=2lgx+2lgy |
| D、2lg(xy)=2lgx•2lgy |
查看答案和解析>>
科目:高中数学 来源: 题型:
| cosA |
| cosB |
| b |
| a |
| 2π |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com