
【题目】如图,在平行四边形ABCD中,∠BAD= ![]() ,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足
,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足 ![]() =λ,其中λ∈[0,1],则
=λ,其中λ∈[0,1],则 ![]() 的取值范围是( )
的取值范围是( ) 
A.[﹣3,﹣1]
B.[﹣3,1]
C.[﹣1,1]
D.[1,3]
【答案】A
【解析】解:建立如图所示的以A为原点, AB,AD所在直线为x,y轴的直角坐标系,
则B(2,0),A(0,0),D( ![]() ,
, ![]() ).
).
∵满足 ![]() =λ,λ∈[0,1],
=λ,λ∈[0,1],![]() =
= ![]() +
+ ![]() =
= ![]() +(1﹣λ)
+(1﹣λ) ![]() =
= ![]() +(1﹣λ)
+(1﹣λ) ![]()
=( ![]() ,
, ![]() )+(1﹣λ)(2,0)
)+(1﹣λ)(2,0)
=( ![]() ﹣2λ,
﹣2λ, ![]() );
);![]() =
= ![]() +
+ ![]() =﹣
=﹣ ![]() +(1﹣λ)
+(1﹣λ) ![]()
=(﹣2,0)+(1﹣λ)( ![]() ,
, ![]() )=(﹣
)=(﹣ ![]() ﹣
﹣ ![]() λ,
λ, ![]() (1﹣λ)),
(1﹣λ)),
则 ![]() =(
=( ![]() ﹣2λ,
﹣2λ, ![]() )(﹣
)(﹣ ![]() ﹣
﹣ ![]() λ,
λ, ![]() (1﹣λ))
(1﹣λ))
=( ![]() ﹣2λ)(﹣
﹣2λ)(﹣ ![]() ﹣
﹣ ![]() λ)+
λ)+ ![]()
![]() (1﹣λ)
(1﹣λ)
=λ2+λ﹣3=(λ+ ![]() )2﹣
)2﹣ ![]() ,
,
因为λ∈[0,1],二次函数的对称轴为:λ=﹣ ![]() ,
,
则[0,1]为增区间,
故当λ∈[0,1]时,λ2+λ﹣3∈[﹣3,﹣1].
故选:A.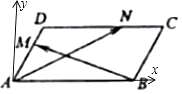


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足
,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足![]() .
.

(1)求椭圆C的方程;
(2)若斜率为k(其中![]() )的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积
)的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年发现,任意三角形的外心、重心、垂心位于同一条直线上,这条直线称为欧拉线已知![]() 的顶点
的顶点![]() ,若其欧拉线的方程为
,若其欧拉线的方程为![]() ,则顶点
,则顶点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的上、下、左、右四个顶点分别为A,B,C,D,x轴正半轴上的点P满足|PA|=|PD|=2,|PC|=4。
(a>b>0)的上、下、左、右四个顶点分别为A,B,C,D,x轴正半轴上的点P满足|PA|=|PD|=2,|PC|=4。
(I)求椭圆C的标准方程以及点P的坐标;
(II)过点P作直线l交椭圆C于点M,N,是否存在这样的直线l使得△MNA和△MND的面积相等?若存在,请求出直线l的方程,若不存在,请说明理由;
(III)在(II)的条件下,求当直线l的倾斜角为钝角时△MND的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔业公司今年初用98万元购进一艘渔船用于捕捞,第一年需各种费用12万
元,从第二年开始包括维修费在内,每年所需费用均比上一年增加4万元,该船每年捕捞的
总收入为50万元.
(1)该船捕捞几年开始盈利(即总收入减去成本及所有费用之差为正值)?
(2)该船捕捞若干年后,处理方案有两种:
①当年平均盈利达到最大值时,以26万元的价格卖出;
②当盈利总额达到最大值时,以8万元的价格卖出.问哪一种方案较为合算,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知关于![]() 的不等式
的不等式![]() ,其中
,其中![]() .
.
(1)当![]() 变化时,试求不等式的解集
变化时,试求不等式的解集![]() ;
;
(2)对于不等式的解集![]() ,若满足
,若满足![]() (其中
(其中![]() 为整数集). 试探究集合
为整数集). 试探究集合![]() 能否为有限集?若 能,求出使得集合
能否为有限集?若 能,求出使得集合![]() 中元素个数最少的
中元素个数最少的![]() 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合![]() ;若不能,请说明理由.
;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点. 
(1)当DE⊥平面VBC时,判断直线DE与平面ABC的位置关系,并说明理由;
(2)当D、E、F分别为线段VA、VC、AB上的中点,且VC=2BC时,求二面角B﹣DE﹣F的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com