
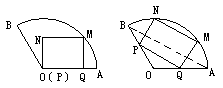
将一块圆心角为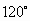 ,半径为20cm的扇形铁片裁成一块矩形,如下图所示有两种裁法:(让矩形一边在扇形的一条半径OA上,如图(1);或让矩形一边与扇形的弦AB平行,如图(2),请问哪一种裁法能得到最大面积的矩形?并求出这个最大值.
,半径为20cm的扇形铁片裁成一块矩形,如下图所示有两种裁法:(让矩形一边在扇形的一条半径OA上,如图(1);或让矩形一边与扇形的弦AB平行,如图(2),请问哪一种裁法能得到最大面积的矩形?并求出这个最大值.
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
| ||
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
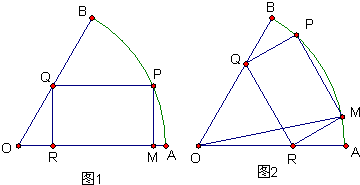
将一块圆心角为![]() ,半径为20cm的扇形铁片裁成一块矩形,如图有两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值。
,半径为20cm的扇形铁片裁成一块矩形,如图有两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
将一块圆心角为![]() ,半径为
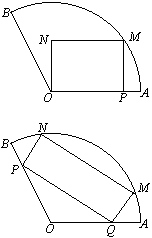
,半径为![]() ㎝的扇形铁片裁成一块矩形,有如图(1)、(2)的两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪 种裁法能得到最大面积的矩形?并求出这个最大值.
㎝的扇形铁片裁成一块矩形,有如图(1)、(2)的两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪 种裁法能得到最大面积的矩形?并求出这个最大值.
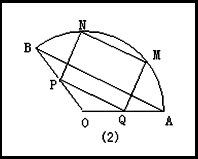

查看答案和解析>>
科目:高中数学 来源: 题型:
课外研究题:将一块圆心角为![]() ,半径为20厘米的扇形铁片裁成一块矩形,请你设计裁法,使裁得矩形的面积最大?并说明理由.
,半径为20厘米的扇形铁片裁成一块矩形,请你设计裁法,使裁得矩形的面积最大?并说明理由.
教学建议:这是一个研究性学习内容,可让学生在课外两人一组合作完成,写成研究报告,在习题课上让学生交流研究结果,老师可适当进行点评。
参考答案:这是一个如何下料的问题,一般有如图(1)、图(2)的两种裁法:即让矩形一边在扇形的一条半径![]() 上,或让矩形一边与弦
上,或让矩形一边与弦![]() 平行。从图形的特点来看,涉及到线段的长度和角度,将这些量放置在三角形中,通过解三角形求出矩形的边长,再计算出两种方案所得矩形的最大面积,加以比较,
平行。从图形的特点来看,涉及到线段的长度和角度,将这些量放置在三角形中,通过解三角形求出矩形的边长,再计算出两种方案所得矩形的最大面积,加以比较,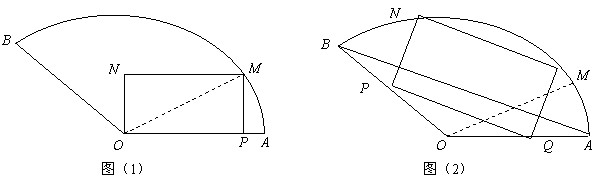 就可以得出问题的结论.
就可以得出问题的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com