
【题目】已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为![]() ,
,![]() .这两条曲线在第一象限的交点为
.这两条曲线在第一象限的交点为![]() ,
,![]() 是以
是以![]() 为底边的等腰三角形.若
为底边的等腰三角形.若![]() ,记椭圆与双曲线的离心率分别为
,记椭圆与双曲线的离心率分别为![]() 、
、![]() ,则
,则![]() 的取值范围是_____.
的取值范围是_____.
【答案】![]()
【解析】
如图所示,设椭圆与双曲线的标准方程分别为:![]() ,
,![]() .(a1,a2,b1,b2>0,a1>b1).根据△PF1F2是以PF1为底边的等腰三角形,|PF1|=10,可得10+2c=2a1,10﹣2c=2a2,可得
.(a1,a2,b1,b2>0,a1>b1).根据△PF1F2是以PF1为底边的等腰三角形,|PF1|=10,可得10+2c=2a1,10﹣2c=2a2,可得![]() ,于是e1+e2=e2
,于是e1+e2=e2![]() f(e2),e2>1.利用导数研究其单调性即可得出.
f(e2),e2>1.利用导数研究其单调性即可得出.
解:如图所示,
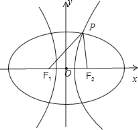
设椭圆与双曲线的标准方程分别为:![]() ,
,![]() .(a1,a2,b1,b2>0,a1>b1)
.(a1,a2,b1,b2>0,a1>b1)
∵△PF1F2是以PF1为底边的等腰三角形,|PF1|=10,
∴10+2c=2a1,10﹣2c=2a2,
相减可得:2c=a1﹣a2,
∴![]() ,
,
∴![]() ,
,
∴e1+e2=e2![]() f(e2),e2>1.
f(e2),e2>1.
∴f′(e2)=1![]() 1
1![]() 0,
0,
∴函数f(e2)在e2>1时单调递增,
∴f(e2)>f(1)=1![]() .
.
∴e1+e2的取值范围是![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若ARB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() ,
,![]() ,连接
,连接![]() 并延长,与轨迹
并延长,与轨迹![]() 交于另一点
交于另一点![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() 是坐标原点,记
是坐标原点,记![]() 与
与![]() 的面积之和为
的面积之和为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的通项公式是
的通项公式是![]() (
(![]() 表示不超过实数
表示不超过实数![]() 的最大整数).
的最大整数).
(1)证明:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 都是数列
都是数列![]() 的项;
的项;
(2)![]() 是否是数列
是否是数列![]() 的项,证明你的结论;
的项,证明你的结论;
(3)证明:有无穷多个2的正整数幂是数列![]() 的项.
的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种候鸟每年都按一定的路线迁徙,飞往繁殖地产卵,科学家经过测量发现候鸟的飞行速度可以表示为函数![]() ,单位是
,单位是![]() ,其中
,其中![]() 表示候鸟每分钟耗氧量的单位数,
表示候鸟每分钟耗氧量的单位数,![]() 为表示测量过程中候鸟每分钟的耗氧偏差.(参考数据:
为表示测量过程中候鸟每分钟的耗氧偏差.(参考数据:![]() ,
,![]() ,
,![]() )
)
(1)若![]() ,候鸟停下休息时,它每分钟的耗氧量为多少个单位?
,候鸟停下休息时,它每分钟的耗氧量为多少个单位?
(2)若雄鸟的飞行速度为![]() ,雌鸟的飞行速度为
,雌鸟的飞行速度为![]() ,那么此时雄鸟每分钟的耗氧量是雌鸟每分钟耗氧量的多少倍?
,那么此时雄鸟每分钟的耗氧量是雌鸟每分钟耗氧量的多少倍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com